��Ŀ����
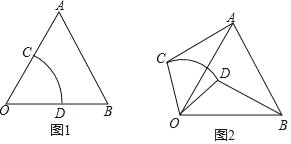
����Ŀ���ڵȱ���AOB�У�������COD��ͼ1�ڷţ�ʹ���εİ뾶OC��OD�ֱ���OA��OB�غϣ�OA=OB=2��OC=OD=1���̶��ȱ���AOB������������COD�Ƶ�O��ʱ����ת���߶�AC��BDҲ��֮�仯������ת��Ϊ������0������360�㣩
��1����OC��ABʱ����ת����=�� ���ȣ�
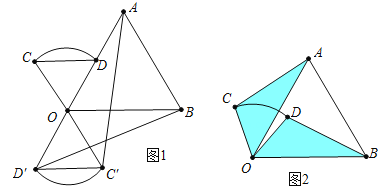
���֣���2���߶�AC��BD�к�������ϵ�������ͼ2����֤����
Ӧ�ã���3����A��C��D���㹲��ʱ����BD�ij���
��չ����4��P���߶�AB������һ�㣬������COD����ת�����У���ֱ��д���߶�PC�����ֵ����Сֵ��
���𰸡���1��60��240��(2) AC=BD�����ɼ���������3��![]() ��
��![]() ����4��PC�����ֵ=3��PC����Сֵ=
����4��PC�����ֵ=3��PC����Сֵ=![]() ��1��
��1��
����������������1����ͼ1������֪����D���߶�AD���߶�AD���ӳ�����ʱ��OC��AB����ʱ��ת����=60����240�㣮
��2��������AC=BD��ֻҪ֤����AOC�ա�BOD���ɣ�
��3����ͼ3��ͼ4�����ֱ���⼴�ɣ�
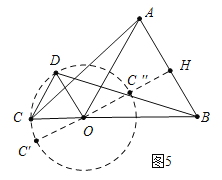
��4����ͼ5��������������C����OΪԲ����1Ϊ�뾶�ġ�O���˶�������O��OH��AB��H��ֱ��OH����O��C�䡢C�壬�߶�CB�ij���ΪPC�����ֵ���߶�C��H�ij���ΪPC����Сֵ����֪PC�����ֵ=3��PC����Сֵ=![]() ��1��
��1��
�������1����ͼ1�У��ߡ�ABC�ǵȱ������������AOB=��COD=60�㣬�൱��D���߶�AD���߶�AD���ӳ�����ʱ��OC��AB����ʱ��ת����=60����240�㣮
�ʴ�Ϊ��60��240��
��2��������AC=BD������������
��ͼ2�У��ߡ�COD=��AOB=60�㣬���COA=��DOB������AOC�͡�BOD����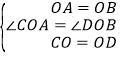 �����AOC�ա�BOD����AC=BD��
�����AOC�ա�BOD����AC=BD��
��3������ͼ3������A��C��D����ʱ����OH��AC��H��
��Rt��COH�У���OC=1����COH=30�㣬��CH=HD=![]() ��OH=
��OH=![]() ����Rt��AOH����AH=
����Rt��AOH����AH=![]() =
=![]() ����BD=AC=CH+AH=
����BD=AC=CH+AH=![]() ��
��
��ͼ4������A��C��D����ʱ����OH��AC��H��
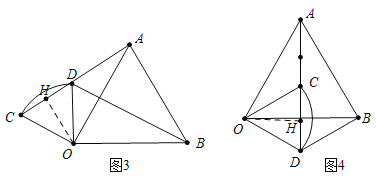
��֪AC=BD=AH��CH=![]() ��
��
������������A��C��D���㹲��ʱ��BD�ij�Ϊ![]() ��
��![]() ��
��
��4����ͼ5��������������C����OΪԲ����1Ϊ�뾶�ġ�O���˶�������O��OH��AB��H��ֱ��OH����O��C�䡢C�壬�߶�CB�ij���ΪPC�����ֵ���߶�C��H�ij���ΪPC����Сֵ����֪PC�����ֵ=3��PC����Сֵ=![]() ��1��
��1��

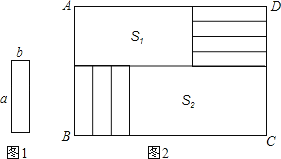
����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ���Ƴ���������ͳ��ͼ��


����������Ϣ�����������������£�
ƽ���ɼ�(��) | ��λ��(��) | ����(��) | ���� | |
�� | a | 7 | 7 | 1.2 |
�� | 7 | b | 8 | c |
��1��д��������a��b��c��ֵ��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա������ɼ�����ѡ������һ������������ΪӦѡ������Ա��