题目内容
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=- x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.

(1)求b,c的值.
(2)结合函数的图象探索:当y>0时x的取值范围.
 x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求b,c的值.
(2)结合函数的图象探索:当y>0时x的取值范围.
(1)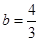 ,c=2;(2)-1<x<3.
,c=2;(2)-1<x<3.
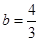 ,c=2;(2)-1<x<3.
,c=2;(2)-1<x<3.试题分析:(1)根据正方形的性质得到B(2,2),C(0,2),然后把B点和C点坐标代入解析式得到关于b、c的方程组,再解方程组即可;
(2)由(1)得到二次函数解析式为y=-
 x2+
x2+ x+2,再求出抛物线与x轴的交点坐标,然后根据图象得到当y>0时x的取值范围.
x+2,再求出抛物线与x轴的交点坐标,然后根据图象得到当y>0时x的取值范围.试题解析:(1)∵正方形OABC的边长为2,
∴B(2,2),C(0,2),
把B(2,2),C(0,2)代入y=-
 x2+bx+c得
x2+bx+c得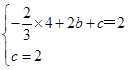 ,解得
,解得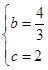 ;
;(2)二次函数解析式为y=-
 x2+
x2+ x+2,
x+2,当y=0时,-
 x2+
x2+ x+2=0,
x+2=0,解得x1=-1,x2=3,
∴抛物线与x轴的交点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0.
考点: 1.待定系数法求二次函数解析式;2.二次函数与不等式(组).

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
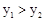 ?
? 的图象向右移动3个单位,再向下移动4个单位,解析式是 ;它的顶点坐标是 .
的图象向右移动3个单位,再向下移动4个单位,解析式是 ;它的顶点坐标是 . 与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
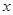 轴的交点坐标.
轴的交点坐标.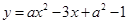 的图象开口向上,并且经过原点
的图象开口向上,并且经过原点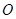
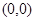 .
.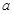 的值;
的值; 的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是( ).
的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是( ).