题目内容
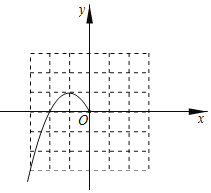
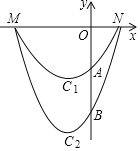
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 与x轴交于点C,与反比例函数
与x轴交于点C,与反比例函数![]() 交于点
交于点![]() 和点B.
和点B.

(1)求反比例函数表达式及点B的坐标;
(2)点P是x轴上的一点,若![]() 的面积是6,求点P的坐标.
的面积是6,求点P的坐标.
【答案】(1)![]() ,(-1,-2);(2)(5,0),(-3,0).
,(-1,-2);(2)(5,0),(-3,0).
【解析】
(1)把![]() 代入
代入![]() ,得点A坐标是:(2,1),从而求出反比例函数解析式,联立一次函数和反比例函数解析式,即可求出点B的坐标;
,得点A坐标是:(2,1),从而求出反比例函数解析式,联立一次函数和反比例函数解析式,即可求出点B的坐标;
(2)先求出C的坐标,设P的坐标为(x,0),则CP=![]() ,作AD⊥x轴,BE⊥x轴,根据三角形的面积公式,列出方程,即可求解.
,作AD⊥x轴,BE⊥x轴,根据三角形的面积公式,列出方程,即可求解.
(1)一次函数![]() 与与反比例函数
与与反比例函数![]() 交于点
交于点![]() 和点B,
和点B,
∴把![]() 代入
代入![]() ,得:m=2-1=1,即:点A坐标是:(2,1),
,得:m=2-1=1,即:点A坐标是:(2,1),
∴k=2×1=2,即:反比例函数解析式:![]() ,
,
∴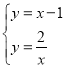 ,即:
,即:![]() ,解得:
,解得:![]() ,
,
∴点B坐标是:(-1,-2)
(2)当有y=0,代入![]() ,得:
,得:![]() ,解得:x=1,
,解得:x=1,
∴点C的坐标是:(1,0)
设P的坐标为(x,0),则CP=![]() ,作AD⊥x轴,BE⊥x轴,
,作AD⊥x轴,BE⊥x轴,
∵![]() 的面积是6,
的面积是6,
∴![]() CP×AD+
CP×AD+![]() CP×BE=6,
CP×BE=6,
∴![]()
![]() ×(1+2)=6,解得:
×(1+2)=6,解得:![]() ,
,
∴点P的坐标是:(5,0),(-3,0).


练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目