题目内容
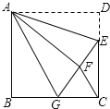
【题目】在正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折到△AFE,延长EF交边BC于点G,连接AG,CF,下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S![]() =
=![]() ,其中正确的有( )个.
,其中正确的有( )个.
A.1B.2C.3D.4
【答案】D
【解析】
①正确,可以根据HL进行证明.
②正确,设BG=GF=x,在RT△EGC中,利用勾股定理即可解决问题.
③正确,根据tan∠AGB=![]() ,tan∠FCM=
,tan∠FCM=![]() 的值即可判定.
的值即可判定.
④正确,根据S△FGC=![]() GCFM即可计算.
GCFM即可计算.
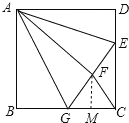 作FM⊥BC于M,
作FM⊥BC于M,
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=6,∠B=∠D=∠BCD=90,
∵△AEF是由△ADE翻折,
∴AD=AF=AB,∠ADE=∠AFE=∠AFG=90,
在RT△AGF和RT△AGB中,
![]()
∴△ABG≌△AFG.故①正确。
∴BG=GF,设BG=GF=x,
在RT△EGC中,∵∠ECG=90,EC=4,EG=x+2,GC=6x,
∴![]() ,
,
∴x=3,
∴BG=GC=3,故②正确。
∵FM∥EC,
∴![]() ,
,
∴FM=![]() ,GC=
,GC=![]() ,CM=
,CM=![]() ,
,
∴tan∠AGB=![]() =2,tan∠FCM=
=2,tan∠FCM=![]() =2,
=2,
∴∠AGB=∠FCM,
∴AG∥CF,故③正确,
∴S△FGC=![]() 3
3![]() =
=![]() ,故④正确。
,故④正确。
故选D.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.