题目内容
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )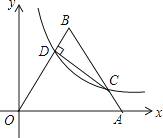
A.25 ![]()
B.18 ![]()
C.9 ![]()
D.9
【答案】C
【解析】解:过点A作AE⊥OB于点E,如图所示.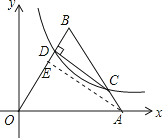
∵△OAB为边长为10的正三角形,
∴点A的坐标为(10,0)、点B的坐标为(5,5 ![]() ),点E的坐标为(
),点E的坐标为( ![]() ,
, ![]() ).
).
∵CD⊥OB,AE⊥OB,
∴CD∥AE,
∴ ![]() .设
.设 ![]() =n(0<n<1),∴点D的坐标为(
=n(0<n<1),∴点D的坐标为( ![]() ,
, ![]() ),点C的坐标为(5+5n,5
),点C的坐标为(5+5n,5 ![]() ﹣5
﹣5 ![]() n).∵点C、D均在反比例函数y=
n).∵点C、D均在反比例函数y= ![]() 图象上,∴
图象上,∴ 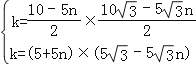 ,解得:
,解得: 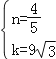 .
.
故选C.
过点A作AE⊥OB于点E,根据正三角形的性质以及三角形的边长可找出点A、B、E的坐标,再由CD⊥OB,AE⊥OB可找出CD∥AE,即得出 ![]() ,令该比例
,令该比例 ![]() =n,根据比例关系找出点D、C的坐标,利用反比例函数图象上点的坐标特征即可得出关于k、n的二元一次方程组,解方程组即可得出结论.本题考查了反比例函数图象上点的坐标特征、平行线的性质以及等边三角形的性质,解题的关键是找出点D、C的坐标.本题属于中档题,稍显繁琐,解决该题型题目时,巧妙的借助了比例来表示点的坐标,根据反比例函数图象上点的坐标特征找出方程组是关键.
=n,根据比例关系找出点D、C的坐标,利用反比例函数图象上点的坐标特征即可得出关于k、n的二元一次方程组,解方程组即可得出结论.本题考查了反比例函数图象上点的坐标特征、平行线的性质以及等边三角形的性质,解题的关键是找出点D、C的坐标.本题属于中档题,稍显繁琐,解决该题型题目时,巧妙的借助了比例来表示点的坐标,根据反比例函数图象上点的坐标特征找出方程组是关键.

【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):请根据上表的内容解答下列问题:
表示立方米):请根据上表的内容解答下列问题:
(1)填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费___________元;
,则应收水费___________元;
(2)若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?
),则应收水费多少元?
价目表
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元/ |
(3)若该户居民![]() 、
、![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 、
、![]() 两个月共交水费多少元?(答案可含有
两个月共交水费多少元?(答案可含有![]() )
)