题目内容
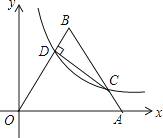
【题目】(题文)如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,△ABD、△BCE均为等边三角形,DE、AB交于点F,AF=3![]() ,则△ACE的面积为_____.
,则△ACE的面积为_____.

【答案】6![]()
【解析】
如图所示,过D作DG⊥AB于G,EK⊥AC交AC的延长线于K,根据等边三角形的性质、勾股定理、30°角直角三角形的性质可得DG=![]() AG,BC=
AG,BC=![]() AC,再证明△ADF≌△GEF,根据全等三角形的性质可得DF=EF,GF=BF,所以FG=
AC,再证明△ADF≌△GEF,根据全等三角形的性质可得DF=EF,GF=BF,所以FG=![]() ,AG=2
,AG=2![]() ,即可得AB=4
,即可得AB=4![]() ,AC=2
,AC=2![]() ,EC=BC=
,EC=BC=![]() AC=6
AC=6![]() ,在Rt△CEK中,EK=
,在Rt△CEK中,EK=![]() EC=3
EC=3![]() ,根据三角形的面积公式求得S△ACE=
,根据三角形的面积公式求得S△ACE=![]() ACEK=6
ACEK=6![]() .
.
如图所示,过D作DG⊥AB于G,EK⊥AC交AC的延长线于K.
∵△ABD是等边三角形,DG⊥AB,
∴AG=BG=![]() AB,由勾股定理得:DG=
AB,由勾股定理得:DG=![]() AG,
AG,
∵∠BAC=30°,
∴AC=![]() AB,
AB,
∴AG=AC=![]() AB,
AB,
∵由勾股定理得:BC=![]() AC,
AC,
∴DG=BC=BE,
∵∠EBA=60°+30°=90°,
∴EB⊥AB.
∴DG∥EB.
∴∠BEF=∠GDF,∠DGB=∠EBF=90°,
在△DGF与△EBF中,
∵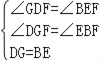 ,
,
∴△ADF≌△GEF(AAS),
∴DF=EF,GF=BF,
∵AG=BG,AF=3![]() ,
,
∴FG=![]() ,AG=2
,AG=2![]() ,
,
∴AB=4![]() ,AC=2
,AC=2![]() ,EC=BC=
,EC=BC=![]() AC=6
AC=6![]() ,
,
在Rt△CEK中,EK=![]() EC=3
EC=3![]() ,
,
∴S△ACE=![]() ACEK=
ACEK=![]() 2
2![]() 3
3![]() =6
=6![]() .
.
故答案为6![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目