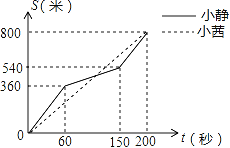
题目内容
【题目】如图，点E是正方形ABCD内的一点，点
在BC边的下方，连接AE，BE，CE，
，
若
，
，
，且
≌
，则
______ 
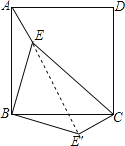
【答案】135
【解析】
先由全等三角形的性质证明△EBE′是等腰直角直角三角形，进而得出∠BEE′=∠BE′E=45°，由勾股定理求出EE′2的值，再勾股定理的逆定理证得△EE′C是直角三角形，从而∠EE′C=90°，即可得出答案．
连接EE′.
∵△ABE≌△CBE′，
∴∠ABE=∠CBE′，
∵四边形ABCD是正方形，
∴∠ABC=90°，
∴∠EBE′=90°，
∴△EBE′是直角三角形，
又∵△ABE≌△CBE′，
∴BE=BE′=2，∠AEB=∠BE′C，
∴∠BEE′=∠BE′E=45°，
∵EE′2=22+22=8，AE=CE′=1，EC=3，
∴EC2=E′C2+EE′2，
∴△EE′C是直角三角形，
∴∠EE′C=90°，
∴∠AEB=135°，
故答案为：135．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
