题目内容
如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BC＝CD，过D作DE∥AB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你说明道理．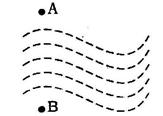
见解析
试题分析：由DE∥AB可得∠A=∠E，再有BC=CD，对顶角相等，即可证得△ABC≌△EDC，从而得到结论.
∵DE∥AB
∴∠A=∠E，
在△ABC和△EDC中，
∠A=∠E，
∠ACB=∠DCE，
BC=CD，
∴△ABC≌△EDC（AAS），
∴AB=DE．
点评：本题属于基础应用题，只需学生熟练掌握全等三角形的判定方法，即可完成．
练习册系列答案
相关题目
≌△
，
，
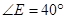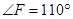，则∠
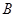等于（ ）
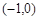，则点C的坐标为 。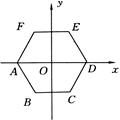
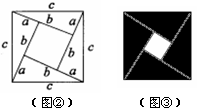
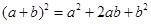，根据图①乙能得到的数学公式是 ．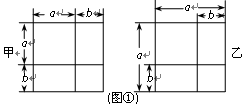
，
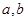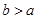，斜边长为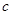
，利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式，这个公式是： ，这就是著名的勾股定理．请利用图②证明勾股定理．
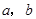，那么
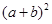的值是 ．