Question

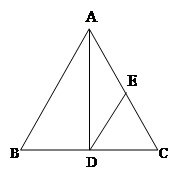
如图：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB=        
   

Answer 1

35°

试题分析：过点E作EF⊥AD，证明△ABE≌△AFE，再求得∠CDE=90°-35°=55°，进而得到∠CDA和∠DAB的度数，即可求得∠EAB的度数．
过点E作EF⊥AD，

∵DE平分∠ADC，且E是BC的中点，
∴CE=EB=EF，
又∵∠B=90°，且AE=AE，
∴△ABE≌△AFE，
∴∠EAB=∠EAF．
又∵∠CED=35°，∠C=90°，
∴∠CDE=90°-35°=55°，
∴∠CDA=110°，
∵∠B=∠C=90°，
∴DC∥AB，
∴∠CDA+∠DAB=180°，
∴∠DAB=70°，
∴∠EAB=35°．
点评：解答本题的关键是根据题意作出辅助线EF⊥AD，构造出全等三角形，再由全等三角形的性质解答．