题目内容
A城有肥料300吨,B城有肥料200吨,现要把这些肥料全部运往甲,乙两乡,从A城往甲,乙两乡运肥料的费用分别为每吨20元和25元;从B城往甲,乙两乡运肥料的费用分别为每吨25元和15元.现甲乡需要肥料260吨,乙乡需要肥料240吨.设从A城运往甲乡的肥料为x吨.
(1)请你填空完成下表中的每一空:
| 调入地 化肥量(吨) 调出地 | 甲乡 | 乙乡 | 总计 |
| A城 | x | _________ | 300 |
| B城 | _________ | _________ | 200 |
| 总计 | 260 | 240 | 500 |
(3)怎样调运化肥,可使总运费最少?最少运费是多少?
(1)填空见下表;(2)y==-15x+13100;(3) A城运往甲乡的化肥为260吨,A城运往乙乡的化肥为40吨,B城运往甲乡的化肥为20吨,B城运往乙乡的化肥为200吨,使总运费最少,最少为9200元
解析试题分析:(1)根据A城运往甲乡的化肥为x吨,则可得A城运往乙乡的化肥为(300-x)吨,B城运往甲乡的化肥为(260-x)吨,B城运往乙乡的化肥为[240-(300-x)]吨;
(2)根据(1)中所求以及每吨运费从而可得出y与x大的函数关系;
(2)x可取60至260之间的任何数,利用函数增减性求出即可.
试题解析:(1)填表如下:
(2)根据题意得出:调入地
化肥量(吨)
调出地甲乡 乙乡 总计 A城 x 300-x 300 B城 260-x 240-(300-x) 200 总计 260 240 500
y=20x+25(300-x)+25(260-x)+15[240-(300-x)]=-15x+13100;
(3)因为y=-15x+13100,y随x的增大而减小,根据题意可得: ,
,
解得:60≤x≤260,
所以当x=260时,y最小,此时y=9200元.
此时的方案为:A城运往甲乡的化肥为260吨,A城运往乙乡的化肥为40吨,B城运往甲乡的化肥为20吨,B城运往乙乡的化肥为200吨,使总运费最少,最少为9200元
考点:1.一次函数的应用;2.一元一次不等式组的应用.

某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
| 原料名称 饮料名称 | 甲 | 乙 |
| A | 20克 | 40克 |
| B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?


 与
与 轴交于点A(
轴交于点A(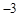 ,0),与
,0),与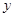 轴交于点B,且与直线
轴交于点B,且与直线 :
: 的交点为C(
的交点为C( ,4) .
,4) .  ,点P(m,n)为直线
,点P(m,n)为直线
 升.
升.
 ,0),且与反比例函数y=
,0),且与反比例函数y= (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
 x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 . 