题目内容
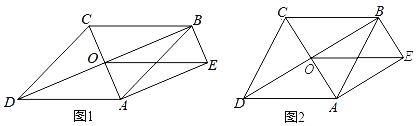
【题目】已知:如图,在Rt△ABC和Rt△ABD中,∠ACB=90°,∠ABD=90°,AB=BD,BC=4,(点A、D分别在直线BC的上下两侧),点G是Rt△ABD的重心,射线BG交边AD于点E,射线BC交边AD于点F.
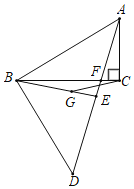
(1)求证:∠CAF=∠CBE;
(2)当点F在边BC上,AC=1时,求BF的长;
(3)若△BGC是以BG为腰的等腰三角形,试求AC的长.
【答案】(1)见解析;(2)BF=![]() ;(3)AC=2或2
;(3)AC=2或2![]() .
.
【解析】
(1)根据重心的定义可得BE是Rt△ABD的中线,然后根据三线合一可得∠AEB=90°,再根据三角形外角的性质即可证出结论;
(2)过点D作DH⊥BC于H,利用AAS证出△ABC≌△BDH,从而可得AC=BH=1,HD=BC=4,然后根据相似三角形的判定证出△AFC∽△DFH,列出比例式即可求出结论;
(3)根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据重心的定义、垂直平分线的判定、全等三角形的判定及性质和勾股定理即可分别求出结论.
(1)∵点G是Rt△ABD的重心,
∴BE是Rt△ABD的中线,
又∵在Rt△ABC中,∠ABD=90°,AB=BD,
∴BE⊥AD,即∠AEB=90°,
∵∠AFB=∠ACF+∠FAC=∠FBE+∠BEF,且∠ACF=∠BEF=90°,
∴∠CAF=∠CBE;
(2)过点D作DH⊥BC于H,
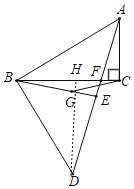
∵∠ABD=90°,
∴∠ABC+∠DBC=90°,且∠ABC+∠BAC=90°,
∴∠BAC=∠DBC,且AB=BD,∠ACB=∠BHD,
∴△ABC≌△BDH(AAS)
∴AC=BH=1,HD=BC=4,
∴HC=3,
∵∠ACB=∠DHC=90°,∠AFC=∠DFH,
∴△AFC∽△DFH,
∴![]() =
=![]()
∴CF=![]() HF,
HF,
∴HF=![]() =
=![]() ,
,
∴BF=BH+HF=1+![]() =
=![]() ;
;
(3)当GC=GB时,如图,连接DG并延长交BC于H,交AB于N,连接NC,
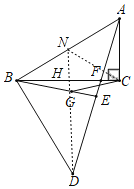
∵点G是Rt△ABD的重心,
∴AN=BN,
∵∠ACB=90°,
∴BN=NC=AN,
∴点N在BC的垂直平分线上,
∵BG=GC,
∴点G在BC的垂直平分线上,
∴DN垂直平分BC,
∴BH=HC=2,DH⊥BC,
∵∠ABD=90°,
∴∠ABC+∠DBC=90°,且∠ABC+∠BAC=90°,
∴∠BAC=∠DBC,且AB=BD,∠ACB=∠BHD,
∴△ABC≌△BDH(AAS)
∴AC=BH=2;
若BG=BC=4,如图,
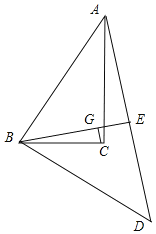
∵点G是Rt△ABD的重心,
∴BG=2GE,
∴GE=2,
∴BE=6,
∵∠ABD=90°,AB=BD,BE⊥AD
∴BE=AE=6,
∴AB=![]() AE=6
AE=6![]() ,
,
∴AC=![]() =
=![]() =2
=2![]() ,
,
综上所述:AC=2或2![]() .
.