Question

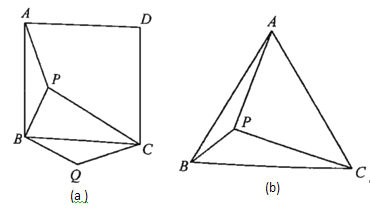
【题目】（1）如图（a）所示，点是正方形内的一点，把绕点顺时针方向旋转，使点与点重合，点的对应点是．若，，，求的度数．

（2）如图（b）所示，点是等边三角形内的一点，若，，，求的度数．

Answer 1

【答案】（1）135°；（2）150°

【解析】

（1）根据题意得出△ABP绕点B顺时针方向旋转了90°，才使点A与C重合，进而得出∠PBQ=90°，再利用勾股定理逆定理得出∠PQC的度数，进而求出∠BQC的度数；

（2）由题意可得出：△ABP绕点B顺时针方向旋转60°，才使点A与C重合，进而得出∠PP'C=90°，即可得出∠BPA的度数．

（1）如图(a)所示，连接．

由旋转可知：，．

又∵四边形是正方形，

∴绕点顺时针方向旋转了90°，才使点与重合．

即，

∴是等腰直角三角形．

∴，．

在中，，，，

∴，

∴．

故．

（2）如图(b)所示，作，且，连接，

∴是等边三角形．∴，．

∵是等边三角形，

∴，，

∴∠ABP+∠PBC=∠PBC+∠CBP'，

∴．∴．

∴，．

在中，，，，

∴，

∴．

故．