题目内容
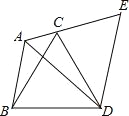
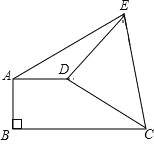
【题目】如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=_____.
【答案】7
【解析】
过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,由旋转的性质可知△CDF≌△EDG,从而有CF=EG,由△ADE的面积可求EG,得出CF的长,由矩形的性质得BF=AD,根据BC=BF+CF即可求解.
过D点作DF⊥BC,垂足为F,过E点作EG⊥AD,交AD的延长线与G点,

由旋转的性质可知CD=ED,
∵∠EDG+∠CDG=∠CDG+∠FDC=90°,
∴∠EDG=∠FDC,又∠DFC=∠G=90°,
∴△CDF≌△EDG,
∴CF=EG,
∵S△ADE=![]() ×AD×EG=6,AD=4,
×AD×EG=6,AD=4,
∴EG=3,则CF=EG=3,
依题意得四边形ABFD为矩形,
∴BF=AD=4,
∴BC=BF+CF=4+3=7,
故答案为:7.

练习册系列答案
相关题目
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?