Question

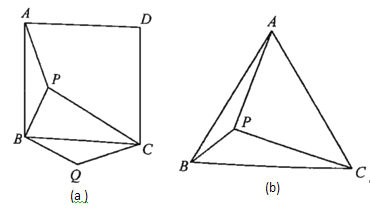
【题目】如图所示，在中，，，，点为内一点，连接、、，且．

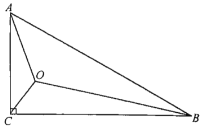
（1）以点为旋转中心，将绕点顺时针方向旋转60°，得到（得到、的对应点分别为点、），按要求画图（保留作图痕迹）．

（2）在（1）的条件下，求的度数及的值．

Answer 1

【答案】（1）见解析；（2）∠A'BC=90°，．

【解析】

（1）在Rt△ABC中，易得∠ABC=30°，由于旋转角为60°，易得旋转后的A'B⊥CB．故过点B作BC的垂线，截取A'B=AB，再以点A'为圆心，以AO为半径画弧，以点B为圆心，以BO为半径画弧，两弧相交于点O'，连接A'O'、BO'，即可得到△A'O'B；

（2）根据旋转的性质求出A'B的长以及△BOO'是等边三角形，根据等边三角形的三条边都相等可得BO=OO'，等边三角形三个角都是60°求出∠BOO'=∠BO'O=60°，然后求出C、O、A'、O'四点共线，再利用勾股定理列式求出A'C，从而得到OA+OB+OC=A'C．

（1）∵∠C=90°，AC=1，BC，

∴AB=，

∴AB=2AC，

∴∠ABC=30°．

∵△AOB绕点B顺时针方向旋转60°，

∠A'BC=∠ABC+60°=30°+60°=90°，

∴A'B⊥CB．

过点B作BC的垂线，截取A'B=AB，

再以点A'为圆心，以AO为半径画弧，

以点B为圆心，以BO为半径画弧，

两弧相交于点O'，连接A'O'、BO'，

即△A'O'B如图所示；

（2））∵∠C=90°，AC=1，BC，

∴AB=，

∴AB=2AC，

∴∠ABC=30°．

∵△AOB绕点B顺时针方向旋转60°，得到△A'O'B，

∴A'B=AB=2，BO=BO'，A'O'=AO，∠ABA′=60°，

∴△BOO'是等边三角形，∠A'BC=∠ABC+∠ABA′=30°+60°=90°，

∴BO=OO'，∠BOO'=∠BO'O=60°．

∵∠AOC=∠COB=∠BOA=120°=∠A'O'B，

∴∠COB+∠BOO'=∠BO'A'+∠BO'O=120°+60°=180°，

∴C、O、A'、O'四点共线．

在Rt△A'BC中，A'C，

∴OA+OB+OC=A'O'+OO'+OC=A'C．