题目内容
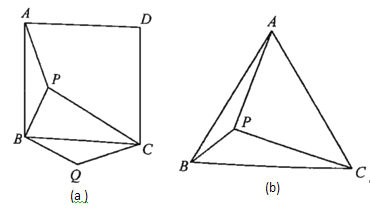
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
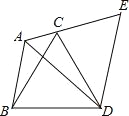
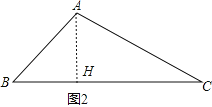
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先利用勾股定理计算出AC=4,然后根据余切的定义求解;
(2)根据余切的定义得到ctan60°=![]() ,然后把tan60°=
,然后把tan60°=![]() 代入计算即可;
代入计算即可;
(3)作AH⊥BC于H,如图2,先在Rt△ACH中利用余切的定义得到ctanC=![]() =2,则可设AH=x,CH=2x,BH=BC﹣CH=20﹣2x,接着再在Rt△ABH中利用勾股定理得到(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
=2,则可设AH=x,CH=2x,BH=BC﹣CH=20﹣2x,接着再在Rt△ABH中利用勾股定理得到(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
解:(1)∵BC=3,AB=5,
∴AC=![]() =4,
=4,
∴ctanB=![]() =
=![]() ;
;
(2)ctan60°=![]() =
=![]() =
=![]() ;
;
(3)作AH⊥BC于H,如图2,
在Rt△ACH中,ctanC=![]() =2,
=2,
设AH=x,则CH=2x,
∴BH=BC﹣CH=20﹣2x,
在Rt△ABH中,∵BH2+AH2=AB2,
∴(20﹣2x)2+x2=102,解得x1=6,x2=10(舍去),
∴BH=20﹣2×6=8,
∴cosB=![]() =
=![]() =
=![]() .
.

【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
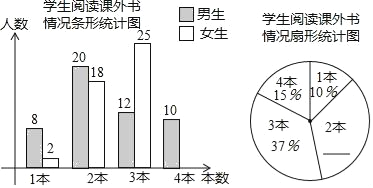
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成![]() 、
、![]() 、
、![]() 、
、![]() 四组,绘制了如下统计图表:
四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
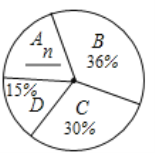
依据以上统计信息,解答下列问题:
(1)求得![]() _____,
_____,![]() ______;
______;
(2)这次测试成绩的中位数落在______组;
(3)求本次全部测试成绩的平均数.