题目内容
【题目】在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,
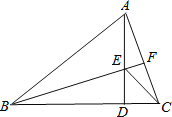
求证:
(1)△ADC≌△BDE;
(2)EA=EC.
【答案】见解析
【解析】
试题分析:(1)直接利用全等三角形的判定方法得出答案;
(2)由条件可求得∠BAC=∠BCA=67.5°,且∠BAD=∠DCE=45°,可得∠EAC=∠ECA=22.5°,可证得结论.
证明:(1)∵AD⊥BC,∠ABC=45°,
∴AD=BD,
在△ADC和△BDE中,
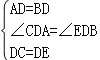 ,
,
∴△ADC≌△BDE(SAS);
(2)∵BA=BC,∠ABC=45°,
∴∠BCA=∠BAC=![]() ×135°=67.5°,
×135°=67.5°,
又∵AD⊥BC,
∴∠ADC=90°,
∵ED=CD,
∴∠ECD=45°,
∴∠ACE=67.5°﹣45°=22.5°,
∵∠AEC=∠EDC+∠ECD=135°,
∴∠EAC=180°﹣22.5°﹣135°=22.5°,
∴EA=EC.

练习册系列答案
相关题目