题目内容
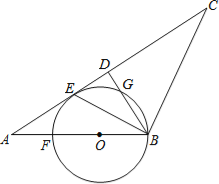
【题目】如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
(1)当△ABC的一边与半圆O相切时,请画出符合题意得图形.
(2)当△ABC的一边与半圆O相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.
【答案】(1)见解析;(2)9π或9![]() +6π.
+6π.
【解析】
试题分析:(1)因为点D,E始终在直线BC,所以当△ABC的一边与半圆O相切时只有三种情况,再分别画出即可;
(2)本题要分当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形分别计算即可.
解:(1)如图所示:
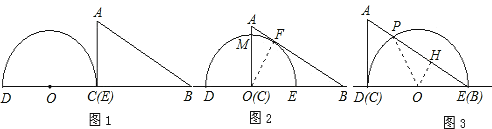
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.
①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:S扇形EOM=![]() π×62=9π(cm2)
π×62=9π(cm2)
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H.
则PH=BH.在Rt△OBH中,∠OBH=30°,OB=6cm
则OH=3cm,BH=3![]() cm,BP=6
cm,BP=6![]() cm,S△POB=
cm,S△POB=![]() ×6
×6![]() ×3=9
×3=9![]() (cm2)
(cm2)
又因为∠DOP=2∠DBP=60°
所以S扇形DOP=6π(cm2)
所求重叠部分面积为:S△POB+S扇形DOP=9![]() +6π(cm2),
+6π(cm2),
综上可知当半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分则重叠部分的面积是9π或9![]() +6π.
+6π.

练习册系列答案
相关题目