Question

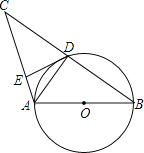
【题目】如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E，连接AD，则下列结论：

①AD⊥BC；②∠EDA=∠B；③OA=AC；④DE是⊙O的切线，正确的个数是（ ）

A．1 个 B．2个 C．3 个 D．4个

Answer 1

【答案】D

【解析】

试题分析：根据直径所对的圆周角是直角推出∠ADB即可判断①；求出OD∥AC，推出DE⊥OD，得出DE是圆O的切线即可判断④；根据线段垂直平分线推出AC=AB，即可判断③，根据切线的性质即可判断②．

解：∵AB是⊙O的直径，

∴∠ADB=90°=∠ADC，

即AD⊥BC，①正确；

连接OD，

∵D为BC中点，

∴BD=DC，

∵OA=OB，

∴DO∥AC，

∵DE⊥AC，

∴OD⊥DE，

∵OD是半径，

∴DE是⊙O的切线，∴④正确；

∴∠ODA+∠EDA=90°，

∵∠ADB=∠ADO+∠ODB=90°，

∴∠EDA=∠ODB，

∵OD=OB，

∴∠B=∠ODB，

∴∠EDA=∠B，∴②正确；

∵D为BC中点，AD⊥BC，

∴AC=AB，

∵OA=OB=AB，

∴OA=AC，∴③正确．

故选D．