题目内容
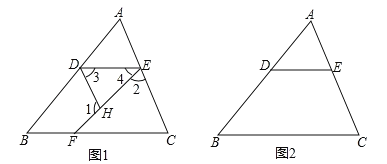
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.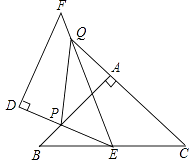
(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
(3)当BP=a,CQ= ![]() a,求PQ长(用含a的代数式表示).
a,求PQ长(用含a的代数式表示).
【答案】
(1)解:∵△ABC和△DEF是两个全等的等腰直角三角形,
∴∠B=∠C=∠DEF=45°,
∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,
∵∠B=∠C=45°,
∴△BPE∽△CEQ,
(2)解:∵△BPE∽△CEQ,
∴ ![]() =
= ![]() ,
,
∵CE=BE,
∴ ![]() =
= ![]() ,
,
∵∠B=∠DEF=45°,
∴△BPE∽△EPQ,
∴∠BPE=∠EPQ,
∴∠DPB=∠DPQ,
∴DP平分∠BPQ.
(3)解:∵△BPE∽△CEQ,
∴ ![]() =
= ![]() ,
,
∵BP=a,CQ= ![]() a,BE=CE,
a,BE=CE,
∴ ![]() =
= ![]() ,
,
∴BE=CE= ![]() a,
a,
∴BC=3 ![]() a,
a,
∴AB=AC=BCsin45°=3a,
∴AQ=CQ﹣AC= ![]() a,PA=AB﹣BP=2a,
a,PA=AB﹣BP=2a,
在Rt△APQ中,PQ= ![]() =
= ![]() a.
a.
【解析】(1)由△ABC和△DEF是两个全等的等腰直角三角形,得出∠B=∠C=∠DEF=45°,由因∠BEP+∠DEF=∠EQC+∠C,所以∠BEP=∠EQC,从而推出△BPE∽△CEQ;
(2) 由相似三角形对应边成比例得出![]() =
=![]() ,又因CE=BE,从而
,又因CE=BE,从而![]() =
=![]() ,又∠B=∠DEF=45°,故△BPE∽△EPQ,根据相似三角形对应角相等得出∠BPE=∠EPQ,从而得出结论;
,又∠B=∠DEF=45°,故△BPE∽△EPQ,根据相似三角形对应角相等得出∠BPE=∠EPQ,从而得出结论;
(3)由相似三角形对应边成比例得出![]() =
=![]() ,从而求出BE=CE=
,从而求出BE=CE= ![]() a,BC=3
a,BC=3 ![]() a,根据锐角三角函数及勾股定理得出结论。
a,根据锐角三角函数及勾股定理得出结论。
【考点精析】关于本题考查的角的平分线判定和全等三角形的性质,需要了解可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);全等三角形的对应边相等; 全等三角形的对应角相等才能得出正确答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
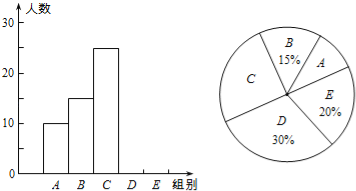
小学生10分钟应用题系列答案【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.