Question

【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．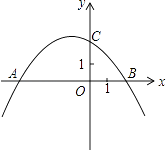

（1）求抛物线的解析式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，当以A、C、D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；
（3）以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．

Answer 1

【答案】
（1）解：如图1，

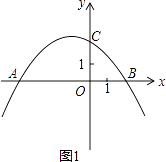
由题可得：

，

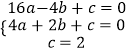解得： ，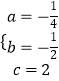

∴抛物线的解析式为y=﹣ x2﹣ x+2；

（2）解：过点D作DH⊥AB于H，交直线AC于点G，如图2．

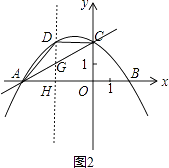
设直线AC的解析式为y=kx+t，

则有 ，

解得： ，

∴直线AC的解析式为y= x+2．

设点D的横坐标为m，则点G的横坐标也为m，

∴DH=﹣ m2﹣ m+2，GH= m+2，

∴DG=﹣ m2﹣ m+2﹣ m﹣2=﹣ m2﹣m，

∴S△ADC=S△ADG+S△CDG

= DGAH+ DGOH= DGAO=2DG

=﹣ m2﹣2m=﹣ （m2+4m）

=﹣ （m2+4m+4﹣4）

=﹣ [（m+2）2﹣4]

=﹣ （m+2）2+2．

∴当m=﹣2时，S△ADC取到最大值2．

此时yD=﹣ ×（﹣2）2﹣ ×（﹣2）+2=2，

即点D的坐标为（﹣2，2）；

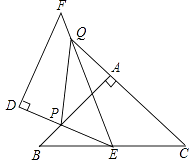
（3）解：设过点E的直线与⊙M相切于点F，与x轴交于点N，连接MF，如图3，

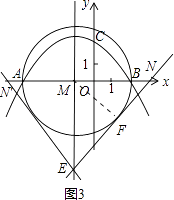
则有MF⊥EN．

∵A（﹣4，0），B（2，0），

∴AB=6，MF=MB=MA=3，

∴点M的坐标为（﹣4+3，0）即M（﹣1，0）．

∵E（﹣1，﹣5），∴ME=5，∠EMN=90°．

在Rt△MFE中，EF= = =4．

∵∠MEF=∠NEM，∠MFE=∠EMN=90°，

∴△MEF∽△NEM，

∴ = ，

∴ = ，

∴NM= ，

∴点N的坐标为（﹣1+ ，0）即（ ，0）或（﹣1﹣ ，0）即（﹣ ，0）．

设直线EN的解析式为y=px+q．

①当点N的坐标为（ ，0）时，

，

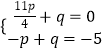解得： ，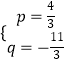

∴直线EN的解析式为y= x﹣ ．

②当点N的坐标为（﹣ ，0）时，

同理可得：直线EN的解析式为y=﹣ x﹣ ．

综上所述：所求直线的解析式为y= x﹣ 或y=﹣ x﹣ ．

【解析】（1）将已知三点的坐标代入抛物线的解析式可得到关于a、b、c的方程组，从而可求得a、b、c的值；
（2）过点D作DH⊥AB，垂足为H，交直线AC于点G，然后再求得AC的解析式，设点D的横坐标为m，则点G的横坐标也为m，从而可以用m的代数式表示出DG，然后用割补法得到△ADC的面积是关于m的二次函数，最后依据二次函数的最值即可；
（3）设过点E的直线与⊙M相切于点F，与x轴交于点N，连接MF，由切线的性质可知：MF⊥EN．然后再求得点M的坐标以及线段ME、MF、EF的长，接下来，再证明△MEF∽△NEM，然后依据相似三角形的性质可求出MN的长度，从而得到点N的坐标，最后，再运用待定系数法求解即可.