��Ŀ����
����Ŀ��ɽ��ʡʵ����ѧ�����廪��ѧ�Ƽ�һ��ѧ�������ݹ涨���Ƽ����������ɱ��꼶200��ѧ������ͶƱ��ÿ��ֻ���Ƽ�һ�ˣ�������ȨƱ����ѡ����Ʊ�����ļס��ҡ������ˣ�ͶƱ���ͳ����ͼ1��
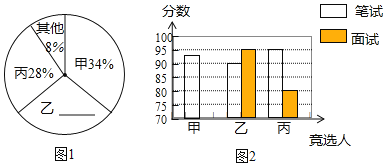
��Σ���������ѡ�˽����˱��Ժ�����������ԣ�����ɼ������ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 92 | 90 | 95 |
���� | 85 | 95 | 80 |
ͼ2��ijͬѧ�����ϱ����Ƶ�һ������ȫ������ͼ���������������Ϣ����������⣺
��1����ȫͼ1��ͼ2��
��2�������ÿ����ѡ�˵ĵ�Ʊ����
��3����ÿ����ѡ�˵�һƱ��1�֣�ͶƱ�����ԡ���������÷ְ���2��5��3�ı�ȷ��������������ѡ�˵�ƽ���ɼ����ɼ��ߵĽ���¼ȡ��Ӧ��¼ȡ˭��
��4����ѧУ��������������ѡ�������ѡ�����μ��廪��ѧ����Ӫ������ұ�ѡ�еĸ��ʣ���Ҫ���б�����״ͼ��
���𰸡���1���𰸼��⣻��2���ף�68���ң�60������56����3��Ӧ��¼ȡ�ң���4��![]() .
.
��������
��1������ͳ��ͼ����1��ȥ�ף�����������ռ�İٷֱȼ�Ϊ����ռ�İٷֱȣ�Ȼ����ݱ����֪�����Գɼ�Ϊ85����ȫ����ͳ��ͼ���ɣ�
��2���ֱ�������200���Ը�����ռ�İٷֱȼ��������Ʊ����
��3�����ռ�Ȩƽ�����ļ��㷽���ֱ������ף��ң�����ƽ���֣�Ȼ�����ѡ��ƽ���ָߵ�¼ȡ��
��4������״ͼ�г����еĿ����ԣ������ҳ����ұ�ѡ�еĿ��ܣ����ø��ʹ�ʽ���㼴��.
�⣺��1��ͼ1���ҵİٷֱȣ�1��8%��28%��34%��30%��
ͼ2�У������Եijɼ�Ϊ85�֣�
��ͼ��
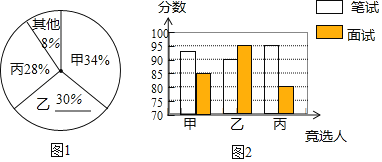
��2����Ʊ���ǣ�200��34%��68��Ʊ����
�ҵ�Ʊ���ǣ�200��30%��60��Ʊ����
����Ʊ���ǣ�200��28%��56��Ʊ����
��3����ƽ���ɼ���![]() ���֣�
���֣�
�ҵ�ƽ���ɼ���![]() ���֣�
���֣�
����ƽ���ɼ���![]() ���֣�
���֣�
���ҵ�ƽ���ɼ���ߣ�
��Ӧ��¼ȡ�ң�
��4������״ͼΪ��
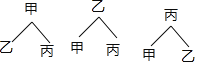
����6�ֵȿ��ܵĽ���������м��ұ�ѡ�еĽ����Ϊ2��
���Լ��ұ�ѡ�еĸ��ʣ�![]()