题目内容
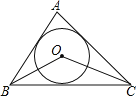
【题目】如图，⊙O是△ABC的内切圆，若∠A＝70°，则∠BOC＝（ ）
A.125°B.115°C.100°D.130°
【答案】A
【解析】
利用三角形内心性质得到∠OBC＝
∠ABC，∠OCB＝∠ACB，则根据三角形内角和得到∠OBC+∠OCB＝（180°﹣∠A），然后利用三角形内角和得到∠BOC＝90°+∠A，再把∠A＝70°代入计算即可．
解：∵⊙O是△ABC的内切圆，
∴OB平分∠ABC，OC平分∠ACB，
∴∠OBC＝∠ABC，∠OCB＝∠ACB，
∴∠OBC+∠OCB＝（∠ABC+∠ACB）＝（180°﹣∠A），
∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣（180°﹣∠A）＝90°+∠A＝180°+×70°＝125°．
故选：A．
练习册系列答案
相关题目
【题目】小明同学利用寒假30天时间贩卖草莓，了解到某品种草莓成本为10元/千克，在第
天的销售量与销售单价如下（每天内单价和销售量保持一致）：
销售量 |
|
销售单价 | 当 |
当 |
设第天的利润
元．
（1）请计算第几天该品种草莓的销售单价为25元/千克？
（2）这30天中，该同学第几天获得的利润最大？最大利润是多少？注：利润＝（售价－成本）×销售量
【题目】为了解某校初三学生上周末使用手机的情况(选项：A.聊天；B.学习；C.购物；D.游戏；E.其他)，随机抽查了该校初三若干名学生，对其上周末使用手机的情况进行统计(每个学生只选一个选项)，绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
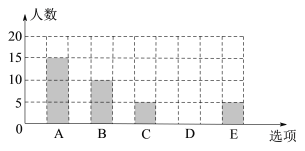
根据以上信息回答下列问题：
(1)这次调查的样本容量是 ；
(2)统计表中m＝ ，n＝ ，补全条形统计图；
(3)若该校初三有540名学生，请估计该校初三学生上周末利用手机学习的人数.
