题目内容
【题目】如图,在矩形ABCD中,AB=1,对角线AC , BD相交于点O,过点O作EF⊥AC,分别交射线AD与射线CB于点E和点F,连接CE,AF.
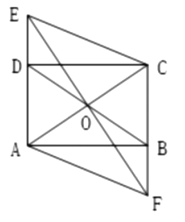
(1)求证:四边形AECF是菱形.
(2)当点![]() 分别在边
分别在边![]() 和
和![]() 上时,设
上时,设![]() ,菱形
,菱形![]() 的面积是
的面积是![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长度.
的长度.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由![]() ,推出EO=OF,又
,推出EO=OF,又![]() ,推出四边形EBFD是平行四边形,再由
,推出四边形EBFD是平行四边形,再由![]() 即可证明四边形
即可证明四边形![]() 是菱形;
是菱形;
(2)由勾股定理表示出AC、AO的值,由cos∠DAC=![]() ,求出AE值,然后根据菱形的性质即可解决问题;
,求出AE值,然后根据菱形的性质即可解决问题;
(3)分![]() 在线段
在线段![]() 延长线上时和
延长线上时和![]() 在线段
在线段![]() 上时两种情形分别讨论求解即可;
上时两种情形分别讨论求解即可;
(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
, ![]() ,
,
在![]() 和
和![]() 中
中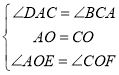 ,
,
![]() ,
, ![]() , 又
, 又![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,且
是平行四边形,且,
∴四边形![]() 是菱形;
是菱形;
(2)由题意得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(3)①当![]() 在线段
在线段![]() 延长线上时,
延长线上时,
![]() 为等腰三角形,
为等腰三角形,
![]() .
.
![]() ,
,
又![]() ,
,
![]() ,
,
解得![]() ;
;
②当![]() 在线段
在线段![]() 上时,
上时,
![]() 为等腰三角形,
为等腰三角形,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() 综上所述:
综上所述:![]() 或
或![]() .
.

练习册系列答案
相关题目
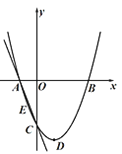
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.