题目内容
阅读理解:对于任意正实数a,b,∵(
-
)2≥0,∴a-2
+b≥0,∴a+b≥2
,只有点a=b时,等号成立.
结论:在a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2
,只有当a=b时,a+b有最小值2
.
根据上述内容,回答下列问题:
(1)若m>0,只有当m=______时,m+
有最小值______;
(2)思考验证:如图,AB为半圆O的直径,C为半圆上任意一点,(与点A,B不重合).过点C作CD⊥AB,垂足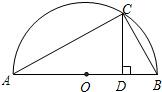 为D,AD=a,DB=b.
为D,AD=a,DB=b.
试根据图形验证a+b≥2
,并指出等号成立时的条件.
| a |
| b |
| ab |
| ab |
结论:在a+b≥2
| ab |
| p |
| p |
根据上述内容,回答下列问题:
(1)若m>0,只有当m=______时,m+
| 1 |
| m |
(2)思考验证:如图,AB为半圆O的直径,C为半圆上任意一点,(与点A,B不重合).过点C作CD⊥AB,垂足
 为D,AD=a,DB=b.
为D,AD=a,DB=b.试根据图形验证a+b≥2
| ab |
(1)∵m+
≥2
,
∴当m=1时,m+
有最小值2;(2分)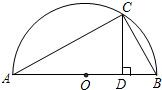
(2)证明:∵AB是直径,
∴∠ACB=90°,
∵CD⊥AB(1分),
∴CD2=AD•BD=ab(2分),
∵CD>0,
∴CD=
(1分),
∵r=
,
∴在Rt△OCD中,r=
>CD,即
>
(1分),
∴a+b>2
(1分),
当CD=r即D与O重合时,
=
,
即a+b=2
,
∴a+b≥2
.(2分)
| 1 |
| m |
m×
|
∴当m=1时,m+
| 1 |
| m |

(2)证明:∵AB是直径,
∴∠ACB=90°,
∵CD⊥AB(1分),
∴CD2=AD•BD=ab(2分),
∵CD>0,
∴CD=
| ab |
∵r=
| a+b |
| 2 |
∴在Rt△OCD中,r=
| a+b |
| 2 |
| a+b |
| 2 |
| ab |
∴a+b>2
| ab |
当CD=r即D与O重合时,
| a+b |
| 2 |
| ab |
即a+b=2
| ab |
∴a+b≥2
| ab |

练习册系列答案
相关题目