题目内容
【题目】如图，直线y=2x+6与反比例函数y= 
（k＞0）的图象交于点A（1，m），与x轴交于点B，平行于x轴的直线y=n（0＜n＜6）交反比例函数的图象于点M，交AB于点N，连接BM．
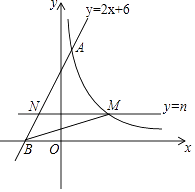
（1）求m的值和反比例函数的表达式；
（2）直线y=n沿y轴方向平移，当n为何值时，△BMN的面积最大？
【答案】
（1）解：∵直线y=2x+6经过点A（1，m），
∴m=2×1+6=8，
∴A（1，8），
∵反比例函数经过点A（1，8），∴8= 
，
∴k=8，
∴反比例函数的解析式为y= 
．
（2）解：由题意，点M，N的坐标为M（ 
，n），N（ 
，n），
∵0＜n＜6，
∴ ＜0，
∴S△BMN= 
×（| |+| |）×n= ×（﹣ + ）×n=﹣ 
（n﹣3）2+ 
，
∴n=3时，△BMN的面积最大．
【解析】（1）先求出点A的坐标A（1，8），利用待定系数法即可得到所求答案；
（2）求二次函数最值问题，先构建二次函数，利用二次函数的性质计算 三角形的面积即可得到答案.
练习册系列答案
名校课堂系列答案
相关题目
【题目】根据实验结果表明，在弹簧的承受范围内，弹簧挂上物体后会伸长，测得一弹簧的长度
与所挂的物体的重量
间有下表的关系，下列说法不正确的是（ ）
| 0 | 1 | 2 | 3 | 4 |
| 20 | 21 | 22 | 23 | 24 |
A.
与
都是变量，且是自变量，是因变量
B.弹簧不挂重物时的长度为
C.随着所挂物体重量的增加，弹簧长度逐渐变长
D.所挂物体的重量每增加
，弹簧长度增加
