题目内容
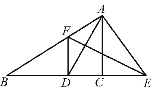
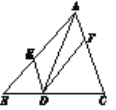
【题目】如图，在△ABC中，点D、E、F分别在边BC、AB、CA上，且DE∥CA，DF∥BA.则下列说法：
①四边形AEDF是平行四边形；
②如果∠BAC＝90°，那么四边形AEDF是矩形；
③如果AD平分∠BAC，那么四边形AEDF是菱形；
④如果∠BAC＝90°，AD平分∠BAC，那么四边形AEDF是正方形．
其中正确的是______(只填写序号)．
【答案】①②③④
【解析】
分别根据平行四边形的判定定理、菱形的判定定理、矩形的判定定理及正方形的判定定理对四个小题进行逐一判断即可．
∵DE∥CA，DF∥BA，
∴四边形AEDF是平行四边形，故①正确；
∵四边形AEDF是平行四边形，∠BAC=90°，
∴四边形AEDF是矩形，故②正确；
∵AD平分∠BAC，四边形AEDF是平行四边形，
∴四边形AEDF是菱形，故③正确；
∵若AD平分∠BAC，则平行四边形AEDF是菱形，
∴若∠BAC=90°，则平行四边形AEDF是正方形，故④正确．
故答案为：①②③④．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
