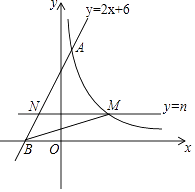题目内容
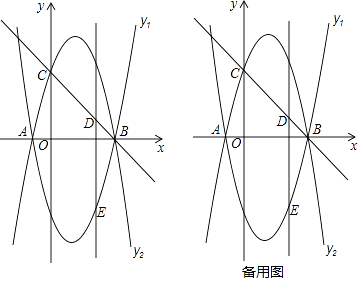
【题目】如图,根据图中信息解答下列问题:
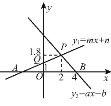
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
【答案】:(1) x<4;(2) x<0;(3)x≤2;(4)2<x<4.
【解析】
(1)求ax+b>0的解集,只需确定直线y2在x轴上方时x的取值范围即可;
(2)求mx+n<1的解集,也就是求直线y1在y=1下方时x的取值范围,据此解答即可;
(3)找出直线y1在直线y2的下方与相交时x的取值范围,据此可确定y1≤y2时x的取值范围;
(4)根据函数图象,找出直线y2在直线y1的下方且在x轴上方时x的取值范围即可.
(1)∵直线y2=ax+b与x轴的交点是(4,0),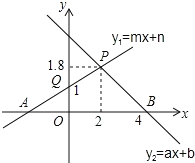
∴当x<4时, y2>0,即不等式ax+b>0的解集是x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时, y1<1,即不等式mx+n<1的解集是x<0;。
(3)由一次函数的图象知,两条直线的交点坐标是(2,1.8),当函数y1的图象在y2的下面时,有x2,
所以当x2时, y1 y2;
(4)如图所示,当2<x<4时,0< y2< y1.
故答案为:(1) x<4; (2) x<0; (3)x≤2; (4)2<x<4.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表
身高分组 | 频数 | 频率 |
152≤ x<155 | 3 | 0.06 |
155≤ x<158 | 7 | 0.14 |
158≤ x<161 | m | 0.28 |
161≤ x<164 | 13 | n |
164≤ x<167 | 9 | 0.18 |
167≤ x<170 | 3 | 0.06 |
170≤ x<173 | 1 | 0.02 |

根据以上统计图表完成下列问题:
(1)统计表中m=____,n=____;并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在什么范围内?