Question

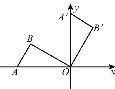
【题目】如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )

A. B.

C. D.

Answer 1

【答案】A

【解析】

利用含30度的直角三角形和勾股定理求出BC和OC，再用旋转的性质得出OC',B'C'，即可解决问题．

解：
在Rt△AOB中，∠AOB=30°，AB=1，
∴OA=2（30°角所对的直角边是斜边的一半）
根据勾股定理得，OB==，
过点B作BC⊥OA于C，
在Rt△BOC中，BC=OB=，根据勾股定理得，OC==，
过点B'作B'C'⊥OA'于C'，
由旋转知，B'C'=BC=，OC'=OC=，，
∴B′点的坐标为（，）．
故选：A．