Question

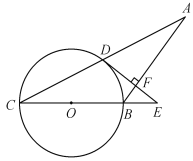
【题目】如图，将两个全等的直角三角尺ABC和ADE如图摆放，∠CAB＝∠DAE＝90°，∠ACB＝∠DEA＝30°，使点D落在BC边上，连结EB，EC，则下列结论：①∠DAC＝∠DCA；②ED为AC的垂直平分线；③EB平分∠AED；④△ACE为等边三角形．其中正确的是（　　）

A.①②③B.①②④C.②③④D.①②③④

Answer 1

【答案】B

【解析】

先利用旋转的性质得到AB＝AC，AC＝AE，则可判断△ABD为等边三角形，所以∠BAD＝∠ADB＝60°，则∠EAC＝∠BAD＝60°，再计算出∠DAC＝30°，于是可对①进行判断；接着证明△AEC为等边三角形得到EA＝EC，得出④正确，加上DA＝DC，则根据线段垂直平分线的判定方法可对②进行判断；然后根据平行线和等腰三角形的性质，则可对③进行判断；即可得出结论．

解：在Rt△ABC中，∵∠ACB＝30°，

∴∠ABC＝60°，

∵△ABC≌△ADE，

∴AB＝AD，AC＝AE，

∴△ABD为等边三角形，

∴∠BAD＝∠ADB＝60°，

∵∠CAB＝∠DAE＝90°

，

∴∠EAC＝∠BAD＝60°，

∵∠BAC＝90°，

∴∠DAC＝30°＝∠ACB，

∴∠DAC＝∠DCA，①正确；

∵AC＝AE，∠EAC＝60°，

∴△ACE为等边三角形，④正确；

∴EA＝EC，

而DA＝DC，

∴ED为AC的垂直平分线，②正确；

∴DE⊥AC，

∵AB⊥AC，

∴AB∥DE，

∴∠ABE＝∠BED，

∵AB≠AE，

∴∠ABE≠∠AEB，

∴∠AEB≠∠BED，

∴EB平分∠AED不正确，故③错误；

故选：B．