题目内容
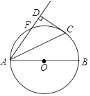
【题目】如图,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于C,D,交AB于E,AF为⊙O的直径,下列结论中正确的有:①∠ABP=∠AOP;②AP=BP;③弧BC=弧DF ;④∠APO=∠BPO;⑤AB⊥PD.
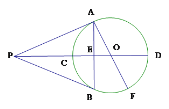
A. ①⑤ B. ②③⑤ C. ①④ D. ①②③④⑤
【答案】D
【解析】
连接OB,根据切线长定理得PA=PB,∠APO=∠BPO;易证得△APO≌△BPO,得∠AOP=∠BOP,即![]() ;再根据这些基础条件进行判断.
;再根据这些基础条件进行判断.
连接OB;
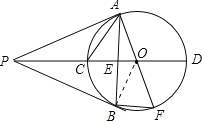
∵PA、PB都是⊙O的切线,
∴PA=PB,∠APO=∠BPO;
又PO=OP,
∴△APO≌△BPO,
∴∠AOP=∠BOP,
∴![]() ;
;
∵PB切⊙O于点B,
∴∠PBA=∠AFB,
由![]() ,得∠AFB=∠AOP,
,得∠AFB=∠AOP,
∴∠PBA=∠AOP,故①正确;
∵PA、PB都是⊙O的切线,
∴PA=PB,故②正确;
∠APO=∠BPO,所以④正确;
∴OP⊥AB,所以⑤正确;
∵∠AOC=∠BOC=∠FOD,
∴![]() ,故③正确.
,故③正确.
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目