题目内容
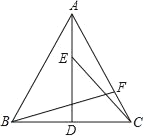
【题目】(1)我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成丁一个大的正方形(如图1),这个矩形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2,称为勾股定理.
证明:∵大正方形面积表示为S=c2,,又可表示为S=4×![]() ab+(b-a)2,
ab+(b-a)2,
∴4×![]() ab+(b-a)2=c2.
ab+(b-a)2=c2.
∴______________
即直角三角形两直角边的平方和等于斜边的平方.
(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论,请你帮助小明完成验证的过程.
(3)如图3所示,∠ABC=∠ACE=90°,请你添加适当的辅助线,证明结论a2+b2=c2.

【答案】(1)![]() ;(2)答案见解析;(3)证明见解析.
;(2)答案见解析;(3)证明见解析.
【解析】
(1)通过化简即可证得;(2)根据四个全等的直角三角形的面积+阴影部分小正方形的面积=大正方形的面积,代入数值,即可证明;(3)作辅助线,构建矩形,根据矩形的面积可得结论.
解答:证明:(1)∵大正方形面积表示为S=![]() ,又可表示为S=4×
,又可表示为S=4×![]() ,
,
∴4×![]() =
=![]() .
.
∴![]() ,
,
∴![]() ,
,
即直角三角形两直角边的平方和等于斜边的平方.
故答案为:![]() ;
;
(2)证明:由图得,大正方形面积=![]() ×ab×4+
×ab×4+![]() =(a+b)×(a+b),
=(a+b)×(a+b),
整理得,![]() ,
,
即![]() ;
;![]()
(3)如图,过A作AF⊥AB,过E作EF⊥AF于F,交BC的延长线于D,则四边形ABDF是矩形,
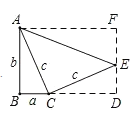
∵△ACE是等腰直角三角形,
∴AC=CE=c,∠ACE=90°=∠ACB+∠ECD,
∵∠ACB+∠BAC=90°,
∴∠BAC=∠ECD,
∵∠B=∠D=90°,
∴△ABC≌△CDE(AAS),
∴CD=AB=b,DE=BC=a,
S矩形ABDF=b(a+b)=2×![]() ,
,
∴![]() .
.

【题目】现如今,通过“微信运动“发布自己每天行走的步数,已成为一种时尚,“健身达人”小华为了了解他的微信朋友圈里大家的“建步走运动“情况,随机抽取了20名好友一天行走的步数,记录如下:
5640 | 6430 | 6320 | 6798 | 7325 | 8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7325 | 6830 | 8648 | 8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)填空:m= ,n= .
(2)补全频数分布直方图.
(3)根据以上统计结果,第二天小华随机查看一名好友行走的步数,试估计该好友的步数不低于7500步(含7500步)的概率.