题目内容
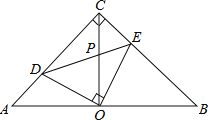
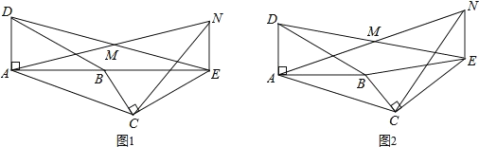
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
【答案】(1)①见解析,②AC=CN,见解析;(2)△BCE绕点B逆时针旋转一周,旋转过程中△CAN为等腰直角三角形时,旋转角度为60°或240°.
【解析】
(1)①先判断出BC=AD,EC=AB,再判断出∠MEN=∠MDA,即可得出结论;②首先证明△MEN≌△MDA,得BC=EN;然后证明△ABC≌△CEN,得到AC=CN;
(2)首先证明△MEN≌△MDA,得BC=EN;然后证明△ABC≌△CEN,得到AC=CN,再判断出∠ACB=90°,进而判断出∠BAC=∠ACB,再由BA≠CB,得出点A,B,C在同一条直线上,即可得出结论.
解:(1)①∵△BAD≌△BCE,
∴BC=AD,EC=AB.
∵EN∥AD,
∴∠MEN=∠MDA.
在△MEN与△MDA中,
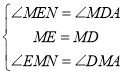
∴△MEN≌△MDA(ASA),
②AC=CN,
由①知,△MEN≌△MDA,
∴EN=AD,
∴EN=BC.
在△ABC与△CEN中,
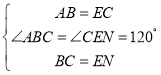
∴△ABC≌△CEN(SAS),
∴AC=CN.
(2)与(1)同理,可证明△MEN≌△MDA,
∴EN=BC.
设旋转角为α,则∠ABC=120°+α,
∠DBE=360°-∠DBA-∠ABC-∠CBE=360°-30°-(120°+α)-60°=150°-α.
∵BD=BE,
![]() ,
,
∵EN∥AD,
∴∠MEN=∠MDA=∠ADB+∠BDE=![]() ,
,
![]() ,
,
∴∠ABC=∠CEN.
在△ABC与△CEN中,
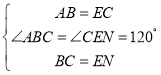 ,
,
∴△ABC≌△CEN(SAS),
∴AC=CN,∠BAC=∠NCE,
∵△CAN能成为等腰直角三角形
∴∠ACN=90°,
∴∠ACB=∠NCE,
∴∠BAC=∠ACB,
∵AB≠CB,
∴点A,B,C在同一条直线上,
此时旋转角为60°.如下图所示:
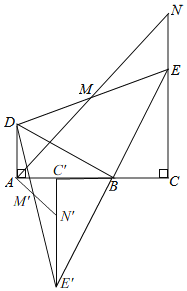
即△BCE绕点B逆时针旋转一周,旋转过程中△CAN为等腰直角三角形时,旋转角度为60°或240°.

 阅读快车系列答案
阅读快车系列答案