题目内容
【题目】已知二次函数y＝ax2+bx+c（a≠0），函数y与自变量x的部分对应值如下表：
x | …… | ﹣1 | 0 | 1 | 4 | …… |
y | …… | 12 | 6 | 2 | 2 | …… |
（1）求二次函数的解析式；
（2）直接写出不等式ax2+bx+c﹣2＞0的解集是 ．
【答案】（1）y＝x2﹣5x+6；（2）x＜1或x＞4．
【解析】
（1）利用待定系数法求抛物线解析式；
（2）由于抛物线经过点（1，2），（4，2），然后写出抛物线在直线y＝2的上方所对应的自变量的范围即可．
解：（1）把（﹣1，12），（0，6），（1，2）代入y＝ax2+bx+c
得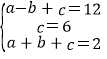
，
解得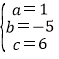
，
所以抛物线解析式为y＝x2﹣5x+6；
（2）因为抛物线经过点（1，2），（4，2），
所以当x＜1或x＞4时，ax2+bx+c＞2，
即不等式ax2+bx+c﹣2＞0的解集为x＜1或x＞4．
故答案为x＜1或x＞4．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某商场用2700元购进甲、乙两种商品共100件，这两种商品的进价、标价如下表所示：
| 甲种 | 乙种 |
进价（元/件） | 15 | 35 |
标价（元/件） | 20 | 45 |
（1）求购进两种商品各多少件？
（2）商品将两种商品全部卖出后，获得的利润是多少元？
