题目内容
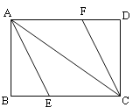
【题目】如图,在矩形ABCD中,AE平分∠BAC交BC于E,CF平分∠ACD交AD于F.
(1)试说明四边形AECF为平行四边形;
(2)探索:当矩形ABCD的边AB和BC满足什么数量关系时,四边形AECF为菱形,并说明理由.
【答案】(1)见解析;(2)当![]() 时,四边形AECF为菱形.
时,四边形AECF为菱形.
【解析】
(1)先证明![]() ,再利用两组对边分别平行的四边形是平行四边形得证.(2)逆向推理,当四边形AECF为菱形时,则有EA=EC,进而可得到∠EAC=∠ACE=30°,
,再利用两组对边分别平行的四边形是平行四边形得证.(2)逆向推理,当四边形AECF为菱形时,则有EA=EC,进而可得到∠EAC=∠ACE=30°,
所以可知![]() .
.
(1)证明:在矩形ABCD中,
AD∥BC,AB∥CD,
∴![]() ,
,
∵AE平分∠BAC,CF平分∠ACD,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴AE∥CF,
又AF∥CE,
∴四边形AECF为平行四边形.
(2)当![]() 时,四边形AECF为菱形.理由如下:
时,四边形AECF为菱形.理由如下:
在Rt△ABC中,![]() ,
,
则∠BAC=60°,∠BCA=30°,
∵AE平分∠BAC,
∴![]() =30°,
=30°,
∴∠EAC=∠ACE=30°,
∴EA=EC,
又由(1)已证,四边形AECF为平行四边形,
∴四边形AECF为菱形.
即,当![]() 时,四边形AECF为菱形.
时,四边形AECF为菱形.

练习册系列答案
相关题目
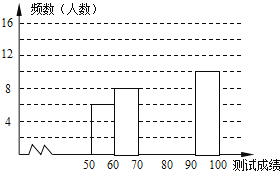
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
![]() 求表中a的值;
求表中a的值; ![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
![]() 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.