题目内容
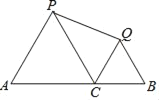
【题目】如图,AB=12,C是线段AB上一点,分别以AC、CB为边在A的同侧作等边△ACP和等边△CBQ,连接PQ,则PQ的最小值是( )
A. 3B. 4C. 5D. 6
【答案】D
【解析】
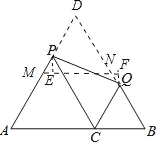
分别延长AP、BQ交于点D,易证四边形CPDQ为平行四边形,得出PD+DQ=PC+CQ=AC+BC=12,作△ABD的中位线MN,则MD=DN=MN=![]() AB,运用中位线的性质和等边三角形的性质求出MD=DN=MN=
AB,运用中位线的性质和等边三角形的性质求出MD=DN=MN=![]() AB,进而求得MD+DN=PD+DQ,得出PM=QN,作PE⊥MN,QF⊥MN,则PE∥QF,然后证得△PME≌△QNF,从而证得MN=EF,根据平行线间的距离得出PQ≥EF,从而求得PQ的最小值.
AB,进而求得MD+DN=PD+DQ,得出PM=QN,作PE⊥MN,QF⊥MN,则PE∥QF,然后证得△PME≌△QNF,从而证得MN=EF,根据平行线间的距离得出PQ≥EF,从而求得PQ的最小值.
解:如图,分别延长AP、BQ交于点D,
∵∠A=∠QCB=60°,
∴AD∥CQ,
∵∠B=CPCA=60°,
∴BD∥PC,
∴四边形CPDQ为平行四边形,
∴PD=CQ,PC=DQ,
∴PD+DQ=PC+CQ=AC+BC=12,
作△ABD的中位线MN,则MD=DN=MN=![]() AB,
AB,
∴MD+DN=AB=12,
∴MD+DN=PD+DQ,
∴PM=QN,
作PE⊥MN,QF⊥MN,
∴PE∥QF,
∴∠PEM=∠QFN=90°,且∠PME=∠QNF=60°,PM=QN
∴△PME≌△QNF(AAS),
∴EM=FN,
∴MN=EF,
∴PQ≥EF,
∴C是线段AB的中点时,PQ的值最小,最小值为![]() AB=6.
AB=6.
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目