题目内容
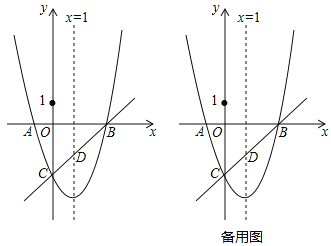
【题目】已知抛物线![]() 与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
与x轴交于点A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求出抛物线的函数表达式;
(2)设点E时抛物线上一点,且S△ABE=![]() S△ABC,求tan∠ECO的值;
S△ABC,求tan∠ECO的值;
(3)点P在抛物线上,点Q在抛物线对称轴上,若以B、C、P、Q为顶点的四边形是平行四边形,求点P坐标。
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)(4,5);(-2,5)(2,-3);
;(3)(4,5);(-2,5)(2,-3);
【解析】
(1)利用抛物线的对称轴方程可计算出b=-2,再把C(0,-3)代入抛物线解析式可得到c=-3,所以抛物线的函数表达式为y=x2-2x-3;
(2)先求得S△ABC=6,然后求得S△ABE=![]() S△ABC=10,进而求得E的纵坐标,代入抛物线的解析式求得E的坐标,过点E作EF⊥y轴于点F,然后在Rt△EOF中,利用正切的定义求解即可;
S△ABC=10,进而求得E的纵坐标,代入抛物线的解析式求得E的坐标,过点E作EF⊥y轴于点F,然后在Rt△EOF中,利用正切的定义求解即可;
(3)此题应分两种情况讨论:
①BC为平行四边形的边;那么将点Q向左或向右平移BC长,即可得到点P的横坐标,再代入抛物线的解析式中求解即可;
②BC为平行四边形的对角线;则P的横坐标为2,再代入抛物线的解析式中求解即可.
解:(1)∵抛物线交y轴于点C,
∴c=-3
又∵对称轴是x=1,
∴![]() =1,解得b=-2,
=1,解得b=-2,
∴抛物线表达式为:y=x2-2x-3;
(2)∵抛物线与x轴交于A、B两点
∴A(-1,0)B(3,0),C(0,-3),
∴AB=4,OC=3,
∴S△ABC=![]() ABOC=6,
ABOC=6,
设点E(x,y)
∵S△ABE=![]() S△ABC,
S△ABC,
∴S△ABE=10,
∴S△ABE=![]() AB|yE|=10,
AB|yE|=10,
即:|y|=5,
∵点E在抛物线上
∴x2-2x-3=5或x2-2x-3=-5,
解得:x=4或x=-2,
∴点E(4,5)或E(-2,5),
过点E作EF⊥y轴于点F,如图1,
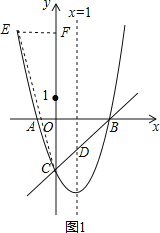
∴EF=4或2,CF=8,
在Rt△EOF中,tan∠ECO=![]() ,
,
∴tan∠ECO=![]() 或tan∠ECO=
或tan∠ECO=![]() .
.
(3)由抛物线的对称轴为x=1,设Q(1,yQ),如图2,
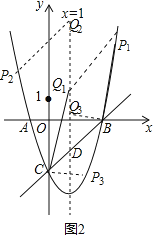
则有:
①若BC为边,
∵B(3,0),C的横坐标与Q的横坐标的差为1,
∴P与B的横坐标的差为1,
∵
∴P的横坐标为4或-2,
则:P(4,yP)或(-2,yP),
把x=4代入抛物线的解析式中,得:y=42-2×4-3=5,
把x=-2代入抛物线的解析式中,得:y=(-202-2×(-2)-3=5,
∴P1(4,5),P2(-2,5);
②若BC为对角线,则P(2,yP),代入抛物线的解析式中,可得:P(2,-3).
综上,存在符合条件的点P,坐标为(4,5)或(-2,5)或(2,-3).