Question

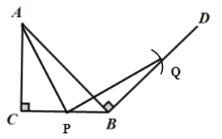
【题目】已知：如图，直角△ABC 中，AC=BC，∠C=90°，∠CAB=∠ABC=45°，过点 B 作射线BD⊥AB 于 B，点 P 为 BC 边上任一点，在射线上取一点 Q，使得 PQ=AP.

（1）请依题意补全图形；

（2）试判断 AP 和 PQ 的位置关系，并加以证明.

Answer 1

【答案】（1）图见解析.（2）垂直，证明见解析.

【解析】

（1）根据题意在CB取点P，再以点P为圆心AP为半径交BD于点Q，连接PQ.

（2）通过证明三角形全等，得到对应角相等，再根据等量代换得到∠APQ=90°即可得到AP与PQ垂直.

（1）

（2）

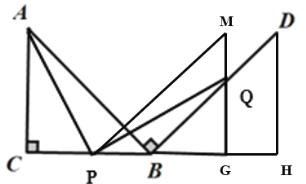
如图作BD=AB，PM∥BD，过点Q作QG垂直于BH，并延长与PM相交于点M.

则三角形PMG与三角形DBH全等

∴PM=BD=AB

又三角形BGQ是等腰直角三角形

∴BG=QG

则PG-BG=MG-QG

即PB=MQ

在三角形PMQ与三角形ABP中

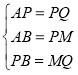
∴（SSS）

∴∠BAP=∠MPQ

又∠BAP+∠CAP=∠MPQ+∠QPG=45°

则∠CAP=∠QPG

∵∠CAP+∠APC=90°

∴∠QPG +∠APC=90°

又∠APQ+(∠QPG +∠APC)=180°

则∠APQ=90°

故AP与PQ垂直.