题目内容
【题目】如图，正方形ABCD的边长是2，点E是CD边的中点，点F是边BC上不与点B，C重合的一个动点，把∠C沿直线EF折叠，使点C落在点C′处．当△ADC′为等腰三角形时，FC的长为_____．
【答案】
或1．
【解析】
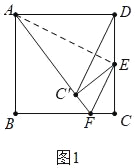
由题意DE=EC=EC′=1，由三角形三条边的关系可知DC′≠DA，所以只要分两种情形讨论即可：①如图1中，当AD=AC′=2时，连接AE．先证△ADE≌△AC′E，再在Rt△ABF中利用勾股定理列方程求解即可；②如图2中，当点F在BC中点时，易证AC′=DC′，满足条件，此时CF=1．
由题意DE=EC=EC′=1，
∴DC′＜1+1
∴DC′≠DA，只要分两种情形讨论即可：
①如图1中，当AD=AC′=2时，连接AE．
∵AE=AE，AD=AC′，DE=DC′，
∴△ADE≌△AC′E，
∴∠ADE=∠AC′E=90°，
∵∠C=∠FC′E=90°，
∴∠AC′E+∠FC′E=180°，
∴A、C′、F共线，设CF=x，则BF=2﹣x，AF=2+x，
在Rt△ABF中，22+（2﹣x）2=（2+x）2，
解得x= ．
②如图2中，当点F在BC中点时，易证AC′=DC′，满足条件，此时CF=1．
综上所述，满足条件的CF的长为或1．
故答案为或1．
练习册系列答案
出彩同步大试卷系列答案
相关题目
