题目内容
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
【答案】
【解析】试题分析:(1)证明:连接OE。
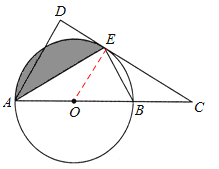
∵CD是⊙O的切线,∴OE⊥CD。
∵AD⊥CD,∴AD∥OE。∴∠DAE=∠AEO。
∵OA=OE,∴∠EAO=∠AEO。
∴∠DAE=∠EAO。∴AE平分∠DAC。
(2)①∵AB是⊙O的直径,∴∠AEB=90°。
∵∠ABE=60°,∴∠EAO=30°。∴∠DAE=∠EAO=30°。
∵AB=6,∴在Rt△ABE中,BE=![]() ="3," AE=
="3," AE=![]()
在Rt△ADE中,∵∠DAE=30°,AE=![]() ,∴
,∴![]() 。
。
②连接OE ∵∠EAO=∠AEO=30°,∴![]() 。
。
∵OA=OB,∴![]() 。
。
∴![]()
![]() 。
。

练习册系列答案
相关题目
【题目】为了解甲、乙两名运动员的体能训练情况,对他们进行了跟踪测试,并把连续十周的测试成绩绘制成如图所示的折线统计图.教练组规定:体能体能测试成绩70分以上(包括70分)为合适. 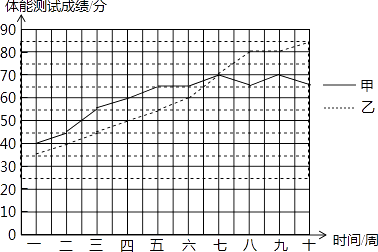
(1)请根据图中所提供的信息填写下表:
平均数 | 中位数 | 体能测试成绩合格次数 | |
甲 | 65 | ||
乙 | 60 |
(2)请从下面两个不同的角度对运动员体能测试结果进行判断: ①依据平均数与成绩合格的次数比较甲和乙,谁的体能测试成绩较好?
②依据平均数与中位数比较甲和乙,谁的体能测试成绩较好?
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.