题目内容
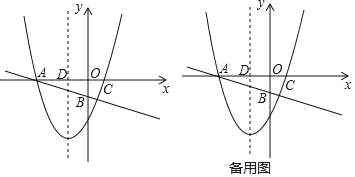
【题目】如图,在直角坐标系中,直线y=﹣![]() x﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.
x﹣1与x轴,y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=x2+bx+c与x轴分别交于点A、C,直线x=﹣1与x轴交于点D.
(1)求抛物线的解析式;
(2)在线段AB上是否存在一点P,使以A,D,P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;如果不存在,请说明理由;
(3)若点Q在第三象限内,且tan∠AQD=2,线段CQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.
【答案】(1)y=x2+2x﹣3;(2)存在;点P坐标为(﹣1,![]() )或(-
)或(-![]() ,-
,-![]() );
);
(3)存在,CQ最小值为![]() .
.
【解析】
(1)根据直线y=﹣![]() x﹣1易求得A点坐标,由抛物线的对称性可求得C点坐标,然后写出抛物线的交点式即可;
x﹣1易求得A点坐标,由抛物线的对称性可求得C点坐标,然后写出抛物线的交点式即可;
(2)根据题意可设点P的坐标为(a,﹣![]() a﹣1),分△AOB∽△APD和△AOB∽△APD两种情况,第一种情况直接根据相似三角形对应边成比例即可求得结果,第二种情况先过点P作PE⊥x轴于点E,则△APE∽△PED,再根据相似三角形对应边成比例即可求得结果;
a﹣1),分△AOB∽△APD和△AOB∽△APD两种情况,第一种情况直接根据相似三角形对应边成比例即可求得结果,第二种情况先过点P作PE⊥x轴于点E,则△APE∽△PED,再根据相似三角形对应边成比例即可求得结果;
(3)如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,﹣![]() )为圆心,因为tan∠AFD=2,
)为圆心,因为tan∠AFD=2,
则连CE交⊙E于点Q,则CQ为满足条件的最小值,再根据两点之间的距离公式求得CE的长,然后减去圆的半径即可得解.
(1)∵直线y=﹣![]() x﹣1与x轴交于A点,
x﹣1与x轴交于A点,
∴点A坐标为(﹣3,0),
又∵直线x=﹣1为对称轴,
∴点C坐标为(1,0),
∴抛物线解析式为:y=(x+3)(x﹣1)=x2+2x﹣3;
(2)存在;
由已知,点D坐标为(﹣1,0),点B坐标为(0,﹣1),
设点P的坐标为(a,﹣![]() a﹣1),
a﹣1),
①当△AOB∽△ADP时,
![]() ,即
,即![]() ,
,
解得:a=﹣1;
点P坐标为(﹣1,![]() );
);
②当△AOB∽△APD时,
过点P作PE⊥x轴于点E,
则△APE∽△PED,
∴PE2=AEED,
∴(﹣![]() a﹣1)2=(a+3)(﹣a﹣1),
a﹣1)2=(a+3)(﹣a﹣1),
解得a1=﹣3(舍去),a2=﹣![]() ,
,
∴点P坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)存在,CQ最小值为![]() ;
;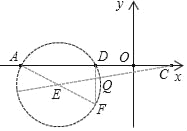
如图,取点F(﹣1,﹣1),过点ADF作圆,则点E(﹣2,﹣![]() )为圆心,
)为圆心,
∵tan∠AFD=2,
∴弧AFD(A、D除外)上的点都是满足条件的Q点,
则连CE交⊙E于点Q,则CQ为满足条件的最小值,
此时CE=![]() ,
,
∵⊙E半径为![]() ,
,
∴CQ最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案