题目内容
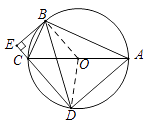
【题目】如图,⊙ ![]() 是△
是△ ![]() 的外接圆,
的外接圆, ![]() 为直径,弦
为直径,弦 ![]() ,
, ![]() 交
交 ![]() 的延长线于点
的延长线于点 ![]() ,求证:
,求证: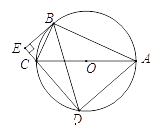
(Ⅰ) ![]() ;
;
(Ⅱ) ![]() 是⊙
是⊙ ![]() 的切线.
的切线.
【答案】解:(Ⅰ)∵四边形ABCD是圆内接四边形,
∴∠ECB=∠BAD.
(Ⅱ)连结OB,OD,
在△ABO和△DBO中,
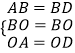 ,
,
∴△ABO≌△DBO(SSS),
∴∠DBO=∠ABO,
∵∠ABO=∠OAB=∠BDC,
∴∠DBO=∠BDC,
∴OB∥ED,
∵BE⊥ED,
∴EB⊥BO,
∴BE是⊙O的切线
【解析】(1)根据圆内接四边形的性质可得结论;
(2)连结OB,OD.易证出△ABO≌△DBO,可得∠DBO=∠ABO,根据半径相等和圆周角定理可得∠ABO=∠OAB=∠BDC,则∠DBO=∠BDC,再由平行线的判定可得OB∥ED,再由BE⊥ED可得证.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目