题目内容
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() .
.

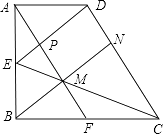
(1)如图![]() ,当
,当![]() 时,将
时,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]() ,
,
①求![]() 的度数;
的度数;
②求证:![]() ;
;
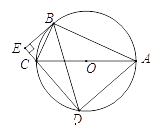
(2)如图![]() ,当
,当![]() 时,猜想
时,猜想![]() 、
、![]() 、
、![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
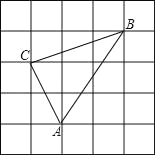
(3)如图![]() ,当
,当![]() ,
,![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的长为________.
的长为________.
【答案】(1)①![]() ,②见解析;(2)
,②见解析;(2)![]() ;见解析,(3)
;见解析,(3)![]() .
.
【解析】
(1)①由旋转得,![]() ,
,![]() ,通过求出∠BAD+∠CAE=30°,即可得答案;②通过证明∠DAF=∠DAE,利用SAS即可证明△ADE≌△ADF;(2)如图,将
,通过求出∠BAD+∠CAE=30°,即可得答案;②通过证明∠DAF=∠DAE,利用SAS即可证明△ADE≌△ADF;(2)如图,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]() 根据等腰直角三角形的性质可得∠C=∠ABC=45°,由旋转的性质可得
根据等腰直角三角形的性质可得∠C=∠ABC=45°,由旋转的性质可得![]() ,
,![]() ,即可证明∠DBF=90°,由(1)可知△ADE≌△ADF,可得DF=DE,根据勾股定理即可得答案;(3)如图,将
,即可证明∠DBF=90°,由(1)可知△ADE≌△ADF,可得DF=DE,根据勾股定理即可得答案;(3)如图,将![]() 绕点
绕点![]() 顺时针旋转120°到△AGB的位置,连接
顺时针旋转120°到△AGB的位置,连接![]() ,过D作DH⊥BG于H,同(2)可得∠GBD=60°,DG=DE,可得∠BDH=30°,利用含30°角的直角三角形的性质可得BH的长,即可得GH的长,利用勾股定理可得DH的长,在Rt△DHG中,利用勾股定理求出DG的长,进而根据△AGD≌△AEC即可得答案.
,过D作DH⊥BG于H,同(2)可得∠GBD=60°,DG=DE,可得∠BDH=30°,利用含30°角的直角三角形的性质可得BH的长,即可得GH的长,利用勾股定理可得DH的长,在Rt△DHG中,利用勾股定理求出DG的长,进而根据△AGD≌△AEC即可得答案.
(1)①由旋转得,![]() ,
,![]() ,
,
∵![]()
∴![]()
②∵∠DAE=30°,∠DAF=30°,
∴∠DAF=∠DAE
在![]() 和
和![]() 中
中

∴![]()
(2)![]()
如图,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]()
∴![]() ,
,![]()
由(1)得![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴在![]() 中,
中,![]()
∴![]()

(3)如图,将![]() 绕点
绕点![]() 顺时针旋转120°到△AGB的位置,连接
顺时针旋转120°到△AGB的位置,连接![]() 过D作DH⊥BG于H,
过D作DH⊥BG于H,
∴BG=CE=5,∠C=∠ABG,
∵∠BAC=120°,AB=AC,
∴∠C=∠ABC=30°,
∴∠GBD=∠ABG+∠ABC=30°+30°=60°,
∵DH⊥BG,
∴∠BDH=30°,
∴BH=![]() BD=4×
BD=4×![]() =2,DH=
=2,DH=![]() =
=![]() =2
=2![]() ,
,
∴GH=BG-BH=5-2=3,
由(1)可知△AGD≌△AEC,
∴DG=DE,
在Rt△DHG中,DG=![]() =
=![]() =
=![]() ,
,
∴DE=DG=![]() .
.

故答案为:![]()

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案