题目内容
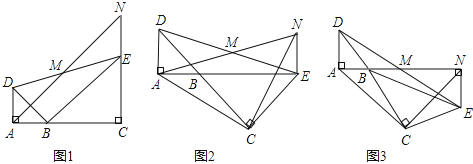
【题目】如图,在正△ABC中,D,E分别在AC,AB上,且 ![]() ,AE=BE,则有( )
,AE=BE,则有( )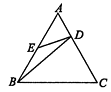
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
【答案】D
【解析】因为△ABC是正三角形,
所以∠A=∠C=60°,
可设AD=a,则AC=3a,而AB=AC=BC=3a,
所以AE=BE= ![]() a,
a,
所以 ![]() =
= ![]() =
= ![]() ,
,
又 ![]() =
= ![]() =
= ![]() ,
,

所以 ![]() =
= ![]() ,∠A=∠C=60°,
,∠A=∠C=60°,
故△AED∽△CBD,故答案为:D.
根据已知结合图形,观察到△AED和△CBD中的∠A=∠C,再证明夹这两个角的两边对应成比例,设AD=a,再分别用含a的代数式表示出AD、AE、DC、BC的长,然后证明AD、AE、DC、BC四条线段成比例,即可得出结论。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目