题目内容
【题目】商场服装柜在销售中发现:某牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存,经市场调查发现,如果每件童装每降价4元,那么平均每天就可多售出8件,
(1)若商场要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
(2)若商场要想平均每天在销售这种童装上盈利最多,那么每件童装应降价多少元?
【答案】(1)每件童装降价20元;(2)当每件童装降价15元时,能获最大利润1250元.
【解析】
(1)设每件童装应降价x元,根据“利润=每件盈利![]() 销量”建立等式方程求解即可;
销量”建立等式方程求解即可;
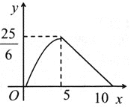
(2)设每件童装应降价x元,利润为y元,根据“利润=每件盈利![]() 销量”可得,y是关于x的一个二次函数,利用二次函数的性质求最值即可.
销量”可得,y是关于x的一个二次函数,利用二次函数的性质求最值即可.
(1)设每件童装应降价x元,则![]()
由题意得:![]()
整理得:![]()
解得:![]()
因为商场的目标是增加盈利,减少库存,所以![]() 舍去,故
舍去,故![]()
答:每件童装降价20元;
(2)设每天销售这种童装利润为y
则![]()
由二次函数的性质得:当![]() 时,y随x的增大而增大;当
时,y随x的增大而增大;当![]() 时,y随x的增大而减小
时,y随x的增大而减小
故当![]() 时,y取得最大值,最大值为1250元
时,y取得最大值,最大值为1250元
答:若商场想平均每天在销售这种童装上盈利最多,每件童装应降价15元.

练习册系列答案
相关题目