题目内容
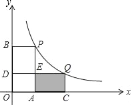
【题目】如图，在平面直角坐标系中，点P（1，2.5）、Q（m，n）在函数y＝
（x＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E，随着m的增大，四边形ACQE的面积（ ）
A. 增大B. 先增大后减小
C. 先减小后增大D. 减小
【答案】A
【解析】
首先利用m和n表示出AC和CQ的长，则四边形ACQE的面积即可利用m、n表示，然后根据函数的性质判断．
解：AC＝m﹣1，CQ＝n
则S四边形ACQE＝ACCQ＝（m﹣1）n＝mn﹣n
∵P（1，2.5）、Q（m，n）在函数
的图象上，
∴mn＝k＝2.5（常数）
∴S四边形ACQE＝2.5﹣n
∴当m＞1时，n随m的增大而减小，
∴S四边形ACQE＝2.5﹣n随m的增大而增大
故选：A．
练习册系列答案
相关题目
