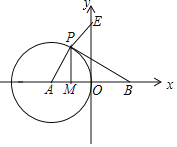Question

【题目】如图，抛物线L：y＝﹣x2+bx+c经过坐标原点，与它的对称轴直线x＝2交于A点．

（1）直接写出抛物线的解析式；

（2）⊙A与x轴相切，交y轴于B、C点，交抛物线L的对称轴于D点，恒过定点的直线y＝kx﹣2k+8（k＜0）与抛物线L交于M、N点，△AMN的面积等于2，试求：

①弧BC的长；

②k的值．

Answer 1

【答案】（1）y＝﹣x2+4x．（2）①；②k=

【解析】

（1）由抛物线的对称轴为直线x＝2及抛物线过原点，即可得出关于b，c的方程组，解之即可求出b，c的值，进而可得出抛物线的解析式；

（2）①连接AB，AC，过点A作AE⊥BC于点E，利用配方法可求出点A的坐标，进而可得出⊙A的半径，在Rt△ABE中，由AE＝AB可得出∠ABE＝30°，进而可得出∠BAE＝60°，由AB＝AC可得出∠BAC＝120°，再利用弧长公式可求出弧BC的长；

②由点A的坐标及⊙A的半径可得出点D的坐标，将x＝2代入y＝kx﹣2k+8中可得出直线y＝kx﹣2k+8过点D，延长NM，交直线x＝2于点D，过点A作AF∥x轴，交DM于点F，过点A作AP⊥DM于点P，在Rt△ADF中，利用面积法可求出AP的长度，联立直线MN和抛物线的解析式成方程组，通过解方程组可求出点M，N的坐标，利用两点间的距离公式可求出MN的长度，再利用三角形的面积公式结合△AMN的面积等于2，可得出关于k的方程，解之即可得出结论．

解：（1）依题意，得：，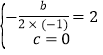

解得：，

∴抛物线的解析式为y＝﹣x2+4x．

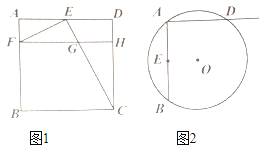
（2）①连接AB，AC，过点A作AE⊥BC于点E，如图1所示．

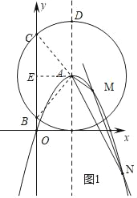
∵y＝﹣x2+4x＝﹣（x﹣2）2+4，

∴点A的坐为（2，4），

∴AB＝AC＝4．

在Rt△ABE中，AB＝4，AE＝2，

∴AE＝AB，

∴∠ABE＝30°，

∴∠BAE＝60°．

∵AB＝AC，

∴∠BAE＝∠CAE，

∴∠BAC＝120°，

∴＝×2πAB＝π．

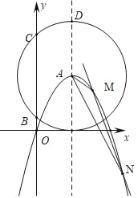
②∵点A的坐为（2，4），AD＝4，

∴点D的坐标为（2，8）．

∵y＝kx﹣2k+8＝k（x﹣2）+8，

∴当x＝2时，y＝kx﹣2k+8＝8，

∴直线y＝kx﹣2k+8过点D．

延长NM，交直线x＝2于点D，过点A作AF∥x轴，交DM于点F，过点A作AP⊥DM于点P，如图2所示．

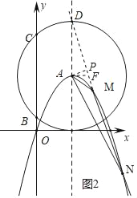
当y＝4时，kx﹣2k+8＝4，

解得：x＝2﹣，

∴点F的坐标为（2﹣，4）．

在Rt△ADF中，AD＝4，AF＝﹣，

∴DF＝，

∴AP＝＝．

联立直线MN和抛物线的解析式成方程组，得：，

解得：，，

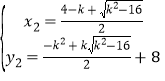∴点M的坐标为（，），点N的坐标为（，），

∴MN＝＝，

∴S△AMN＝APMN＝2，即××＝2，

∴k2﹣16＝1，

解得：k1＝-，k2＝（舍去），

∴k的值为-．