题目内容
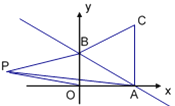
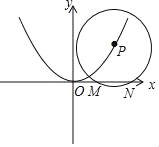
【题目】如图,⊙P的圆心P(m,n)在抛物线y=![]() 上.
上.
(1)写出m与n之间的关系式;
(2)当⊙P与两坐标轴都相切时,求出⊙P的半径;
(3)若⊙P的半径是8,且它在x轴上截得的弦MN,满足0≤MN≤2![]() 时,求出m、n的范围.
时,求出m、n的范围.
【答案】(1)n=![]() m2;(2)⊙P的半径为2;(3)
m2;(2)⊙P的半径为2;(3)![]() ≤m≤4或﹣4≤m≤﹣
≤m≤4或﹣4≤m≤﹣![]() ;7≤n≤8.
;7≤n≤8.
【解析】
(1)将点P(m,n)代入抛物线解析式y=![]() x2可得m与n之间的关系式;
x2可得m与n之间的关系式;
(2)根据⊙P与两坐标轴都相切知|m|=![]() m2 ,解之可得m的值,但要根据实际情况取舍,从而得出⊙P的半径;
m2 ,解之可得m的值,但要根据实际情况取舍,从而得出⊙P的半径;
(3)作PK⊥MN于点K,连接PM,分别求出MN=0和MN=2![]() 时PK的值,据此可得PK=
时PK的值,据此可得PK=![]() m2的范围是7≤
m2的范围是7≤![]() m2≤8,解不等式即可.
m2≤8,解不等式即可.
解:(1)∵点P(m,n)在抛物线y=![]() 上,
上,
∴n=![]() m2;
m2;
(2)当点P(m,![]() m2)在第一象限时,
m2)在第一象限时,
由⊙P与两坐标轴都相切知m=![]() m2,
m2,
解得:m=0(舍)或m=2,
∴⊙P的半径为2;
当点P(m,![]() m2)在第三象限时,
m2)在第三象限时,
由⊙P与两坐标轴都相切知﹣m=![]() m2,
m2,
解得:m=0或m=﹣2,
∴⊙P的半径为2;
(3)如图,作PK⊥MN于点K,连接PM,

当MN=2![]() 时,MK=
时,MK=![]() MN=
MN=![]() ,
,
∵PM=8,
则PK=![]() =
=![]() =7,
=7,
当MN=0时,PK=8,
∴7≤PK≤8,即7≤n≤8,
∵n=![]() m2,
m2,
∴7≤![]() m2≤8,
m2≤8,
解得:![]() ≤m≤4或﹣4≤m≤﹣
≤m≤4或﹣4≤m≤﹣![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目