题目内容
如图,圆O1、圆O2的圆心O1、O2在直线l上,圆O1的半径为2 cm,圆O2的半径为3 cm,O1O2="8" cm。圆O1以1 cm/s的速度沿直线l向右运动,7s后停止运动,在此过程中,圆O1与圆O2没有出现的位置关系是
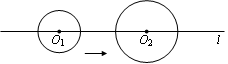

| A.外切 | B.相交 | C.内切 | D.内含 |
D。
⊙O1以1 cm/s的速度沿直线l向右运动,7s后停止运动,此时,O1O2="1" cm。
根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,
∵⊙O1和⊙O2的半径分别为2㎝和3㎝,且O1O2=1㎝,
∴3-2=1,即两圆圆心距离等于两圆半径之差。
∴此时⊙O1和⊙O2的位置关系是内切。
∴在整个运动过程中,⊙O1和⊙O2的位置关系经过了相离、外切、相交和内切,没有内含。故选D。
根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,
∵⊙O1和⊙O2的半径分别为2㎝和3㎝,且O1O2=1㎝,
∴3-2=1,即两圆圆心距离等于两圆半径之差。
∴此时⊙O1和⊙O2的位置关系是内切。
∴在整个运动过程中,⊙O1和⊙O2的位置关系经过了相离、外切、相交和内切,没有内含。故选D。

练习册系列答案
相关题目




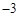






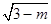 为二次根式,则m的取值为
为二次根式,则m的取值为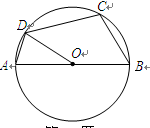
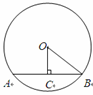
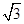 ,OC=1,则OB的长为 .?
,OC=1,则OB的长为 .?