题目内容
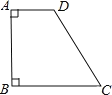
【题目】已知：如图，四边形
中，
，
．在
边上求作点
，则
的最小值为（ ）
A.
B.
C.
D.
【答案】B
【解析】
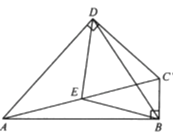
作D点关于AB的对称点D'，连接CD'交AB于P，根据两点之间线段最短可知此时PC+PD最小；再作D'E⊥BC于E，则EB=D'A=AD，先根据等边对等角得出∠DCD'=∠DD'C，然后根据平行线的性质得出∠D'CE=∠DD'C，从而求得∠D'CE=∠DCD'，得出∠D'CE=30°，根据30°角的直角三角形的性质求得D'C=2D'E=2AB，即可求得PC+PD的最小值．
作D点关于AB的对称点D'，连接CD'交AB于P，P即为所求，此时PC+PD=PC+PD'=CD'，根据两点之间线段最短可知此时PC+PD最小．
作D'E⊥BC于E，则EB=D'A=AD．
∵CD=2AD，
∴DD'=CD，
∴∠DCD'=∠DD'C．
∵∠DAB=∠ABC=90°，
∴四边形ABED'是矩形，
∴DD'∥EC，D'E=AB=3，
∴∠D'CE=∠DD'C，
∴∠D'CE=∠DCD'．
∵∠DCB=60°，
∴∠D'CE=30°，
∴D'C=2D'E=2AB=2×3=6，
∴PC+PD的最小值为6．
故选：B．
练习册系列答案
计算高手系列答案
相关题目
【题目】我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售，按计划10辆汽车都要装满，且每辆汽车只能装同一种苗木，由信息解答以下问题：
苗 木 品 种 | A | B | C |
每辆汽车运载量（吨） | 12 | 10 | 8 |
每吨苗木获利（万元） | 3 | 4 | 2 |
（1）设装A种苗木车辆数为x，装运B种苗木的车辆数为y，求y与x之间的函数关系式；
（2）若装运每种苗木的车辆都不少于2辆，则车辆安排方案有几种？写出每种安排方案
（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润．
