题目内容
【题目】如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,tan∠ACD=![]() ,AB=5,那么CD的长是_____.
,AB=5,那么CD的长是_____.
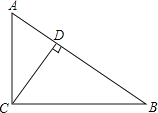
【答案】2.4
【解析】根据余角的性质得到∠B=∠ACD,由tan∠ACD=![]() ,得到tan∠B=
,得到tan∠B=![]() =
=![]() ,设AC=3x,BC=4x,根据勾股定理得到AC=3,BC=4,根据三角形面积的公式即可得到结论.
,设AC=3x,BC=4x,根据勾股定理得到AC=3,BC=4,根据三角形面积的公式即可得到结论.
解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=∠BCD+∠B=90°,
∴∠B=∠ACD,
∵tan∠ACD=![]() ,
,
∴tan∠B=![]() =
=![]() ,
,
设AC=3x,BC=4x,
∵AC2+BC2=AB2,
∴(3x)2+(4x)2=52,
解得x=1,
∴AC=3,BC=4,
∵S△ABC=![]() AB×CD=
AB×CD=![]() AC×BC,
AC×BC,
∴CD=![]() =2.4,
=2.4,
故答案为:2.4.
“点睛”本题考查了解直角三角形,勾股定理,三角形的面积公式,熟记三角形的面积公式是解题的关键.

练习册系列答案
相关题目
【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1)按表格数据格式,表中的a=;b=;
(2)请估计:当次数s很大时,摸到白球的频率将会接近;
(3)请推算:摸到红球的概率是(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.